题目内容
已知[x)表示大于x的最小整数,例如[3)=4,[-1.3)=-1,定义f(x)=[x)-x,则下列命题中正确的是( )
①[x)+[y)≤x+y;
②函数f(x)=[x)-x的值域是(0,1];
③f(x)为R上的奇函数,且f(x)为周期函数;
④若x∈(1,2015),则方程[x)-x=
有2014个根.
①[x)+[y)≤x+y;
②函数f(x)=[x)-x的值域是(0,1];
③f(x)为R上的奇函数,且f(x)为周期函数;
④若x∈(1,2015),则方程[x)-x=
| 1 |
| 2 |
| A、②④ | B、③④ | C、①④ | D、②③ |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用
分析:①,令x=3,y=-1.3,根据“[x)表示大于x的最小整数”,判断①即可;
②,分“当x为整数时”与“当x不为整数时”讨论,依据“[x)”的含义,判断②即可;
③,当x为整数时,-x也是整数,f(-x)=f(x)=1,判断③即可;
④,利用周期函数的概念可判断出f(x)为1为周期的函数,并求出当x∈[0,1)时,f(x)=[x)-x=1-x,作出函数图象,判断④即可.
②,分“当x为整数时”与“当x不为整数时”讨论,依据“[x)”的含义,判断②即可;
③,当x为整数时,-x也是整数,f(-x)=f(x)=1,判断③即可;
④,利用周期函数的概念可判断出f(x)为1为周期的函数,并求出当x∈[0,1)时,f(x)=[x)-x=1-x,作出函数图象,判断④即可.
解答:
解:对于①,令x=3,y=-1.3,则[x)+[y)=[3)+[-1.3)=4-1=3,x+y=3+(-1.3)=1.7,[x)+[y)>x+y,故①错误;
对于②,当x为整数时,f(x)=[x)-x=(x+1)-x=1;
当x不为整数时,f(x)=[x)-x∈(0,1);
所以,函数f(x)=[x)-x的值域是(0,1],故②正确;
对于③,当x为整数时,-x也是整数,f(-x)=f(x)=1,不是奇函数,故③错误;
对于④,因为f(x+1)=[x+1)-(x+1)=([x)+1)-(x+1)=[x)-x=f(x),
所以,f(x)为1为周期的函数,
又当x=0时,f(x)=1,当x∈(0,1)时,f(x)=[x)-x=1-x,
故其图象如下:
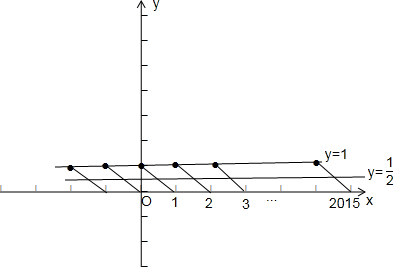
当x∈(1,2015),直线y=
与f(x)=[x)-x有2014个交点(每个周期一个,有2014个周期),
则方程[x)-x=
有2014个根,故④正确.
综上所述,命题中正确的是②④,
故选:A.
对于②,当x为整数时,f(x)=[x)-x=(x+1)-x=1;
当x不为整数时,f(x)=[x)-x∈(0,1);
所以,函数f(x)=[x)-x的值域是(0,1],故②正确;
对于③,当x为整数时,-x也是整数,f(-x)=f(x)=1,不是奇函数,故③错误;
对于④,因为f(x+1)=[x+1)-(x+1)=([x)+1)-(x+1)=[x)-x=f(x),
所以,f(x)为1为周期的函数,
又当x=0时,f(x)=1,当x∈(0,1)时,f(x)=[x)-x=1-x,
故其图象如下:

当x∈(1,2015),直线y=
| 1 |
| 2 |
则方程[x)-x=
| 1 |
| 2 |
综上所述,命题中正确的是②④,
故选:A.
点评:本题考查新定义“[x)”的理解与应用,着重考查函数的周期性、奇偶性、单调性与值域,理解“[x)”的含义是关键,考查转化思想与作图能力,是难题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知函数f(x)=
,则f[f(-3)]=( )
|
| A、-1 | B、1 | C、-3 | D、3 |