题目内容
已知数列{an}中,a1=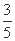 ,an=2-
,an=2-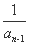 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn=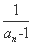 (n∈N*).
(n∈N*).
(1) 求证:数列{bn}是等差数列;
(2) 求数列{an}中的最大项和最小项,并说明理由.
(1) 因为an=2-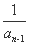 (n≥2,n∈N*),bn=
(n≥2,n∈N*),bn=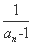 ,
,
所以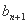 -bn=
-bn=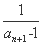 -
-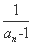
=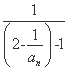 -
-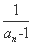
=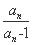 -
-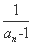 =1.
=1.
又b1=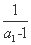 =-
=-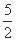 ,所以数列{bn}是以-
,所以数列{bn}是以-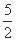 为首项、1为公差的等差数列.
为首项、1为公差的等差数列.
(2) 由(1)知bn=n-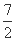 ,则an=1+
,则an=1+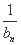 =1+
=1+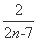 ,
,
设f(x)=1+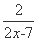 ,则f(x)在区间
,则f(x)在区间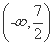 和
和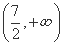 上为减函数.
上为减函数.
故当n=3时,an取得最小值-1;当n=4时,an取得最大值3.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
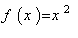 确定t的值,使S1与S2之和最小。
确定t的值,使S1与S2之和最小。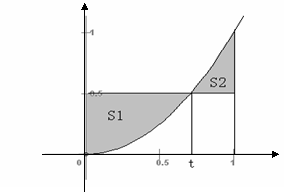
 天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,则每批应生产产品多少件?
天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,则每批应生产产品多少件?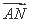 ·
·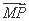 的取值范围.
的取值范围.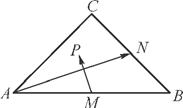
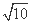 ,求圆O的半径OC的长.
,求圆O的半径OC的长.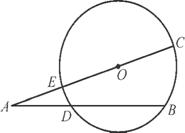
 对应的变换作用下得到的对应点分别为A'(0,0),B'(
对应的变换作用下得到的对应点分别为A'(0,0),B'(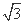 ,1),C'(0,2),求矩阵M.
,1),C'(0,2),求矩阵M.