题目内容
已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.
(1) 若m=4,求直线l被圆C所截得弦长的最大值;
(2) 若直线l是圆心C下方的切线,当a在(0,4]上变化时,求m的取值范围.
(1) 因为x2+y2+2ax-2ay+2a2-4a=0,
即(x+a)2+(y-a) 2=4a,
所以圆心为C(-a,a),半径为r=2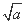 .
.
设直线l被圆C所截得的弦长为2t,圆心C到直线l的距离为d,m=4时,直线l:x-y+4=0,
圆心C到直线l的距离d=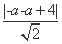 =
=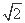 |a-2|,
|a-2|,
t2=(2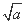 )2-2(a-2)2=-2a2+12a-8
)2-2(a-2)2=-2a2+12a-8
=-2(a-3)2+10,又0<a≤4,
所以当a=3时,t2最大为10,t最大为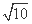 ,即直线l被圆C所截得弦长的值最大,其最大值为2
,即直线l被圆C所截得弦长的值最大,其最大值为2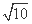 .
.
(2) 圆心C到直线l的距离
d=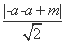 =
=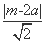 ,
,
因为直线l是圆C的切线,所以d=r,即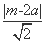 =2
=2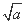 ,
,
所以m=2a±2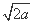 .
.
因为直线l在圆心C的下方,所以-a-a+m<0,m<2a,
所以m=2a-2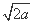 =(
=(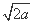 -1)2-1,
-1)2-1,
因为a∈(0,4],所以m∈[-1,8-4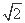 ].
].

练习册系列答案
相关题目
 个单位长度,所得图象的函数解析式为 .
个单位长度,所得图象的函数解析式为 .  ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.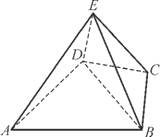
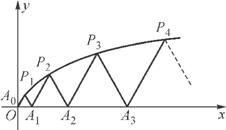
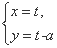 (t为参数)过椭圆C:
(t为参数)过椭圆C: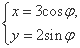 (φ为参数)的右顶点,求常数a的值.
(φ为参数)的右顶点,求常数a的值. 的定义域为( )
的定义域为( )