Question

【题目】如图，在矩形ABCD中，AB＝4，AD＝2，E是CD的中点，现以AE为折痕将△DAE向上折起，D变为D'，使得平面D'AE⊥平面ABCE．

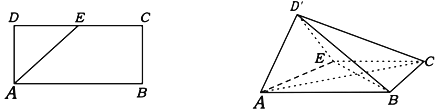
（1）求证：平面ABD'⊥平面BD'E；

（2）求直线CE与平面BCD'所成角的正弦值．

Answer 1

【答案】（1）见解析（2）．

【解析】

（1）证明AE⊥BE，BE⊥AD'，结合D′E⊥AD′，推出AD′⊥面BD′E，然后明面ABD′⊥面BD′E．

（2）建立空间直角坐标系，求出平面BCD′的法向量，利用空间向量的数量积求解直线CE与平面BCD'所成角的正弦值即可．

（1）证明：AE＝BE，AB＝4，

∴AB2＝AE2+BE2，∴AE⊥BE，

∵平面D′AE⊥平面ABCE，且交线为AE，

∴BE⊥平面D'AE，又平面，∴BE⊥AD'，

又D′E⊥AD′，AE∩D′E＝E，∴AD′⊥面BD′E，∵AD′面ABD′，

∴面ABD′⊥面BD′E．

（2）解：取中点为，连接，因为，则，又平面D′AE⊥平面ABCE，且交线为AE，所以平面ABCE，

如图建立空间直角坐标系，

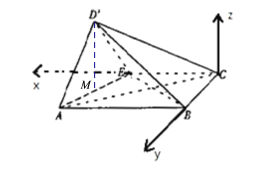
则A(4，2，0)、C(0，0，0)、B(0，2，0)、，E(2，0，0)，

从而（2，0，0），，．

设为平面BCD′的法向量，

则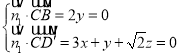，取，则，，所以．

，

故直线CE与平面所成角的正弦值为．