题目内容
向量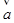 = (cosθ, sinθ),
= (cosθ, sinθ),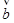 = (
= (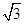 , 1),则
, 1),则 的最大值为( )
的最大值为( )
| A.3 | B.4 | C.5 | D.6 |
B
解析试题分析: =16,所以
=16,所以 =4.
=4.
考点:数量积的性质。
点评:熟记数量积的性质;向量的平方就等于它的模的平方,即 。当求向量的模时经常用到此公式。
。当求向量的模时经常用到此公式。

练习册系列答案
相关题目
设两个向量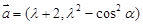 和
和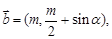 其中
其中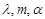 为实数.若
为实数.若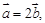 则
则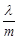 的取值范围是 ( )
的取值范围是 ( )
A.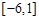 | B.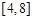 | C. | D. |
设P是 所在平面上一点,且满足
所在平面上一点,且满足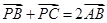 ,若
,若 的面积为1,则
的面积为1,则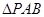 的面积为( )
的面积为( )
A.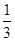 | B. | C.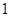 | D.2 |
向量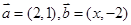 ,若
,若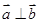 ,则
,则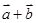 = ( )
= ( )
| A.(3,-1) | B.(-3,1) | C.(-2,-1) | D.(2 ,1) |
若 三点共线 则m的值为
三点共线 则m的值为
A. | B. | C.-2 | D.2 |
设向量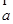 =(1,-3),
=(1,-3), 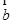 =(-2,4),
=(-2,4), 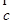 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4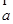 ,4
,4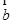 -2
-2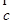 ,2(
,2(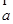 -
-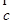 ),
),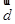 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量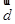 为( )
为( )
| A.(2,6) | B.(-2,6) | C.(2,-6) | D.(-2,-6) |
在△ABC中,∠C=90°, =(k,1),
=(k,1), 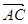 =(2,3),则k的值是( )
=(2,3),则k的值是( )
| A.5 | B.-5 | C. | D.- 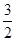 |
如图所示的方格纸中有定点 ,则
,则 ( )
( )
A. | B. | C. | D. |
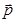 =(sinA,b+c),
=(sinA,b+c),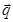 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足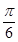 B.
B.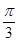 C.
C.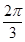 D.
D.