题目内容
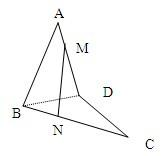11、如图，空间四边形ABCD中，M、N分别是DA、BC上的点，且AM：MD=BN：NC=1：2．又AB=3，CD=6，MN与AB、CD所成的角分别为α，β，则α，β之间的大小关系为（ ）分析：过M点作MP∥AB，连接PN，易得∠PMN是MN与AB所成角，∠PNM是MN与CD所成角，在三角形PMN内求出此角即可．
解答：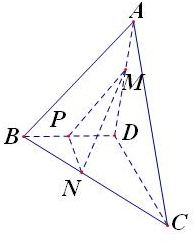
解：如图
过M点作MP∥AB，连接PN，
AM：MD=BP：DP=BN：NC=1：2
∴PN∥CD，∠PMN是MN与AB所成角，∠PNM是MN与CD所成角
∵AB=3，CD=6∴MP=2，PN=2
∴∠PMN=∠PNM 所以α=β，
故选C．
解：如图过M点作MP∥AB，连接PN，
AM：MD=BP：DP=BN：NC=1：2
∴PN∥CD，∠PMN是MN与AB所成角，∠PNM是MN与CD所成角
∵AB=3，CD=6∴MP=2，PN=2
∴∠PMN=∠PNM 所以α=β，
故选C．
点评：本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
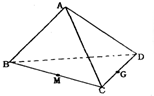如图，空间四边形ABCD中，M、G分别是BC、CD的中点，则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，空间四边形ABCD的对棱AD、BC成60°的角，且AD=BC=4，平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H．
如图，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且
如图，空间四边形ABCD中，E、F分别是AB、AD的中点，G、H分别在BC、CD上，且BG：GC=DH：HC=1：2