题目内容
 如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.
如图,空间四边形ABCD的对棱AD、BC成60°的角,且AD=BC=4,平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H.(1)求证:四边形EFGH为平行四边形;
(2)E在AB的何处时截面EFGH的面积最大?最大面积是多少?
分析:(1)利用线面平行的判定与性质,证出EF∥GH且EH∥FG,从而得到四边形EGFH的两组对边分别平行,即四边形EFGH为平行四边形.
(2)由异面直线所成角的定义,得到∠HGF=60°或120°,利用正弦定理的面积公式得到SEFGH=
GH•GF,再利用平行线分线段成比例定理和基本不等式,证出GH•GF的最大值为4,当且仅当E为AB的中点时取到最大值.由此即可算出截面EFGH的面积最大值,得到本题答案.
(2)由异面直线所成角的定义,得到∠HGF=60°或120°,利用正弦定理的面积公式得到SEFGH=
| ||
| 2 |
解答:解:(1)∵BC∥平面EFGH,BC?平面ABC,平面ABC∩平面EFGH=EF,
∴BC∥EF.同理可得BC∥GH,可得EF∥GH,
同理得到EH∥FG,
∴四边形EGFH中,两组对边分别平行,
因此,四边形EFGH为平行四边形.
(2)∵AD与BC成60°角,
∴平行四边形EFGH中∠HGF=60°或120°,
可得截面EFGH的面积S=GH•GF•sin∠HGE=
GH•GF
∵设
=λ,则
=1-λ
∴GH=λBC=4λ,BC=λAD=4-4λ
可得GH•GF=16λ(1-λ)≤16×[
]2=4
当且仅当λ=
时等号成立
由此可得:当E为AB的中点时,截面EFGH的面积最大,最大值为2
.

∴BC∥EF.同理可得BC∥GH,可得EF∥GH,
同理得到EH∥FG,
∴四边形EGFH中,两组对边分别平行,
因此,四边形EFGH为平行四边形.
(2)∵AD与BC成60°角,
∴平行四边形EFGH中∠HGF=60°或120°,
可得截面EFGH的面积S=GH•GF•sin∠HGE=
| ||
| 2 |
∵设
| GH |
| BC |
| FG |
| AD |
∴GH=λBC=4λ,BC=λAD=4-4λ
可得GH•GF=16λ(1-λ)≤16×[
| λ+(1+λ) |
| 2 |
当且仅当λ=
| 1 |
| 2 |
由此可得:当E为AB的中点时,截面EFGH的面积最大,最大值为2
| 3 |
点评:本题给出三棱锥平行于一组对棱的截面,求证四边形是平行四边形并求面积最大值.着重考查了线面平行的判定与性质、平行线分线段成比例定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
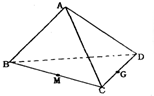 如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则
如图,空间四边形ABCD中,M、G分别是BC、CD的中点,则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点. 如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且
如图,空间四边形ABCD中,AB、BC、CD的中点分别是P、Q、R,且 如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2
如图,空间四边形ABCD中,E、F分别是AB、AD的中点,G、H分别在BC、CD上,且BG:GC=DH:HC=1:2