题目内容
偶函数f(x)在[-1,0]上单调递减,α,β为锐角三角形两内角,则不等式恒成立的是
- A.f(sinα)>f(sinβ)
- B.f(cosα)>f(cosβ)
- C.f(sinα)>f(cosβ)
- D.f(sinα)<f(cosβ)
C
分析:由“偶函数y=f(x)在[-1,0]上为单调递减函数”可知f(x)在[0,1]上为单调递增函数,再由“α、β为锐角三角形的两内角”可得到α+β> ,转化为
,转化为  >α>
>α> -β>0,两边再取正弦,可得1>sinα>sin(
-β>0,两边再取正弦,可得1>sinα>sin( 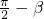 )=cosβ>0,由函数的单调性可得结论.
)=cosβ>0,由函数的单调性可得结论.
解答:∵偶函数y=f(x)在[-1,0]上为单调递减函数
∴f(x)在[0,1]上为单调递增函数
又α、β为锐角三角形的两内角
∴α+β>
∴ >α>
>α> -β>0
-β>0
∴1>sinα>sin(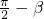 )=cosβ>0
)=cosβ>0
∴f(sinα)>f(cosβ)
故选C.
点评:本题主要考查奇偶性和单调性的综合运用,还考查了三角函数的单调性.属中档题.
分析:由“偶函数y=f(x)在[-1,0]上为单调递减函数”可知f(x)在[0,1]上为单调递增函数,再由“α、β为锐角三角形的两内角”可得到α+β>
 ,转化为
,转化为  >α>
>α> -β>0,两边再取正弦,可得1>sinα>sin(
-β>0,两边再取正弦,可得1>sinα>sin( 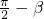 )=cosβ>0,由函数的单调性可得结论.
)=cosβ>0,由函数的单调性可得结论.解答:∵偶函数y=f(x)在[-1,0]上为单调递减函数
∴f(x)在[0,1]上为单调递增函数
又α、β为锐角三角形的两内角
∴α+β>

∴
 >α>
>α> -β>0
-β>0∴1>sinα>sin(
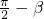 )=cosβ>0
)=cosβ>0∴f(sinα)>f(cosβ)
故选C.
点评:本题主要考查奇偶性和单调性的综合运用,还考查了三角函数的单调性.属中档题.

练习册系列答案
相关题目
已知偶函数f(x)在区间[0,+∞)单调递增,则满足f(
)<f(x)的x取值范围是( )
| x+2 |
| A、(2,+∞) |
| B、(-∞,-1)∪(2,+∞) |
| C、[-2,-1)∪(2,+∞) |
| D、(-1,2) |
已知定义域为R的偶函数f(x)在(-∞,0]上是减函数,且f(
)=0,则不等式f(log2x)>0的解集为( )
| 1 |
| 2 |
A、(0,
| ||||||
B、(
| ||||||
C、(0,
| ||||||
D、(0,
|