题目内容
11.半径为2的球面上有三点A,B,C,满足$AB=2\sqrt{3},BC=2,AC=2\sqrt{2}$,若P为球面上任意一点,则三棱锥P-ABC体积的最大值为$2\sqrt{2}$.分析 由题意画出图形,可知△ABC为球内接直角三角形,连接三角形外接圆的圆心与球心交球于P,求出三棱锥的高,则三棱锥P-ABC体积的最大值可求.
解答 解:如图,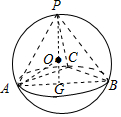
∵$AB=2\sqrt{3},BC=2,AC=2\sqrt{2}$,
∴AC⊥BC,设球心为O,AB的中点为G,连接GO并延长交球于P,
此时三棱锥P-ABC体积的最大,
连接OA,在Rt△OGA中,则OG=$\sqrt{O{A}^{2}-A{G}^{2}}=\sqrt{{2}^{2}-(\sqrt{3})^{2}}=1$.
则PG=3,
∴三棱锥P-ABC体积的最大值为V=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2×3=2\sqrt{2}$.
故答案为:$2\sqrt{2}$.
点评 本题考查棱柱、棱锥、棱台体积的求法,考查了空间想象能力和思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.某产品的广告费用x(百万元)与销售额y(百万元)的统计数据如表:
根据表中数据,用最小二乘法得出y与x的线性回归方程为$\stackrel{∧}{y}$=8.6x+5,则表中的m的值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 25 | 33 | m | 55 | 75 |
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
3.已知a=2-1.2,b=log36,c=log510,则a,b,c的大小关系是( )
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
| A. | (1,$\frac{3}{2}$) | B. | (1,2) | C. | ($\frac{3}{2}$,+∞) | D. | (2,+∞) |
 中新网2016年12月19日电 根据预报,今天开始雾霾范围将进一步扩大,19日夜间至20日,雾霾最严重的时段部分地区PM2.5浓度峰值会超过500微克/立方米,而此轮雾霾最严重的时候,将有包括京津翼、山西、陕西、河南等11个省市在内的地区被雾霾笼罩,PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区在2016年12月19日至28日每天的PM2.5监测数据的茎叶图如图所示:
中新网2016年12月19日电 根据预报,今天开始雾霾范围将进一步扩大,19日夜间至20日,雾霾最严重的时段部分地区PM2.5浓度峰值会超过500微克/立方米,而此轮雾霾最严重的时候,将有包括京津翼、山西、陕西、河南等11个省市在内的地区被雾霾笼罩,PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区在2016年12月19日至28日每天的PM2.5监测数据的茎叶图如图所示: