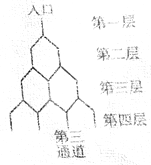
题目内容
【题目】已知某算法的算法框图如图所示，若将输出的（x，y）值依次记为（x1 ， y1），（x2 ， y2），…，（xn ， yn），…，则程序结束时，共输出（x，y）的组数为（ ） 
A.1006
B.1007
C.1008
D.1009
【答案】B
【解析】解：根据程序框图的运算流程，模拟程序的运行，可得： 当n=1时，输出第1对，
当n=3时，输出第2对，
…
当n=2013时，输出最后一对为第1007对，此时，n=2015，满足条件n＞2014，结束．
所以程序结束时，共输出（x，y）的组数为1007．
故选：B．
【考点精析】通过灵活运用程序框图，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明即可以解答此题．
练习册系列答案
相关题目
【题目】为加快新能源汽车产业发展，推进节能减排，国家对消费者购买新能源汽车给予补贴，其中对纯电动乘用车补贴标准如下表：
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R（公里） | ||
80≤R＜150 | 150≤R＜250 | R≥250 | |
纯电动乘用车 | 3.5万元/辆 | 5万元/辆 | 6万元/辆 |
某校研究性学习小组，从汽车市场上随机选取了M辆纯电动乘用车，根据其续驶里程R（单次充电后能行驶的最大里程）作出了频率与频数的统计表：
分组 | 频数 | 频率 |
80≤R＜150 | 2 | 0.2 |
150≤R＜250 | 5 | x |
R≥250 | y | z |
合计 | M | 1 |
（Ⅰ）求x，y，z，M的值；
（Ⅱ）若从这M辆纯电动乘用车中任选2辆，求选到的2辆车续驶里程都不低于150公里的概率；
（Ⅲ）若以频率作为概率，设X为购买一辆纯电动乘用车获得的补贴，求X的分布列和数学期望EX．
