题目内容
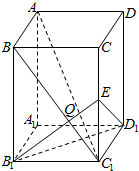
12.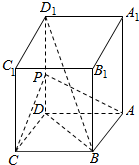 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.(1)求三棱锥P-ACD的体积;
(2)求点D到平面PAC的距离.
分析 (1)由知得PD⊥平面ACD,PD=1,由此能求出三棱锥P-ACD的体积.
(2)设点D到平面PAC的距离为h,由VD-PAC=VP-ACD,能求出点D到平面PAC的距离.
解答 解:(1)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,
∴PD⊥平面ACD,PD=1,${S}_{△ACD}=\frac{1}{2}×1×1$=$\frac{1}{2}$,
∴三棱锥P-ACD的体积V=$\frac{1}{3}×{S}_{△ACD}×PD$=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
(2)∵长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,
∴PC=PA=$\sqrt{1+1}$=$\sqrt{2}$,AC=$\sqrt{1+1}$=$\sqrt{2}$,
∴${S}_{△PAC}=\frac{1}{2}×\sqrt{2}×\sqrt{2}×sin60°$=$\frac{\sqrt{3}}{2}$,
设点D到平面PAC的距离为h,
∵VD-PAC=VP-ACD,
∵三棱锥P-ACD的体积V=$\frac{1}{6}$.
∴$\frac{1}{3}×{S}_{△PAC}×h=\frac{1}{6}$,
∴h=$\frac{\frac{1}{6}}{\frac{1}{3}×\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$.
∴点D到平面PAC的距离为$\frac{\sqrt{3}}{3}$.
点评 本题考查三棱锥的体积的求法,考查点到平面的距离的求法,是基础题,解题时要认真审题,注意等体积法的合理运用.

练习册系列答案
相关题目
8.在正三棱柱ABC-A1B1C1中,已知AB=2,D是棱BB1的中点,且BD=1,则C1与平面ADC的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
3.从空间一点P向二面角α-L-β的两个面α,β分别作垂线PE,PF,E、F为垂足,若∠EPF=30°,则二面角α-L-β的平面角的大小是( )
| A. | 30° | B. | 150° | C. | 30°或150° | D. | 不确定 |
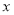 的方程
的方程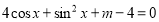 恒有实数解,则实数
恒有实数解,则实数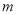 的取值范围是( )
的取值范围是( )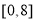 B.
B. 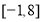 C.
C.  D.
D. 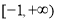
 如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.
如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.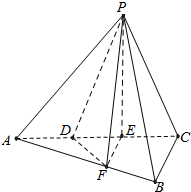 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥面PBC.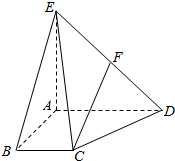 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.