题目内容
12.已知函数f(x)=xlnx.(Ⅰ)求这个函数的图象在点x=1处的切线方程;
(Ⅱ)讨论函数f(x)在区间(0,t](t>0)上的单调性.
分析 (Ⅰ)求出函数f(x)的定义域求出导函数,求这个函数在x=1处的切线的斜率,然后求解函数的切线方程.(Ⅱ)通过f'(x)=1+lnx=0,求出极值点,通过(1)当$0<t≤\frac{1}{e}$时,(2)当$t>\frac{1}{e}$时,分别判断函数的单调性.
解答 (本题满分12分)
解:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=1+lnx.
这个函数的图象在x=1处的切线的斜率为k=f′(1)=1.
把x=1代入f(x)=xlnx中得f(1)=0,即切点坐标为(1,0).
则这个函数的图象在x=1处的切线方程为y=x-1.…(5分)
(Ⅱ)令f′(x)=1+lnx=0,得$x=\frac{1}{e}$.
(1)当$0<t≤\frac{1}{e}$时,在区间(0,t]上,f′(x)≤0成立,所以函数f(x)为减函数.
(2)当$t>\frac{1}{e}$时,在区间$({0,\frac{1}{e}})$上,f′(x)<0,f(x)为减函数;
在区间$({\frac{1}{e},t})$上,f′(x)>0,f(x)为增函数.…(12分)
点评 本题考查函数的导数的综合应用,切线方程以及函数的单调性的判断,考查计算能力.

练习册系列答案
相关题目
2.双曲线$\frac{{y}^{2}}{4}$-x2=1的一条渐近线的方程为( )
| A. | y=2x | B. | y=4x | C. | y=$\frac{1}{2}$x | D. | y=$\frac{1}{4}$x |
20.下列命题中,说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “0<x<$\frac{1}{2}$”是“x(1-2x)>0”的必要不充分条件 | |
| C. | 命题“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
17.阳澄湖大闸蟹的上市规格为:特级雄蟹≥200g,雄蟹≥150g,一级雄蟹≥150g,雌蟹≥125g;二级雄蟹≥125g,雌蟹≥100g.现从某批上市的大闸蟹中随机抽取100只,得到的数据如下:
(1)根据雌雄按分层抽样的方法从这100只大闸蟹中抽取20只,若雌蟹有8只,求a,b的值;
(2)按样本估计总体的方法从这批上市的大闸蟹中有放回地随机抽取3只,记特级雄蟹的只数为X,求X的数学期望.
| 雄蟹 | 雌蟹 | |||||
| 等级 | 特级 | 一级 | 二级 | 特级 | 一级 | 二级 |
| 只数 | 30 | a | 10 | 20 | 10 | b |
(2)按样本估计总体的方法从这批上市的大闸蟹中有放回地随机抽取3只,记特级雄蟹的只数为X,求X的数学期望.
4.若空间向量$\overrightarrow{a}$=(1,-2,1),$\overrightarrow{b}$=(1,0,2),则下列向量可作为向量$\overrightarrow{a}$,$\overrightarrow{b}$所在平面的一个法向量的是( )
| A. | (4,-1,2) | B. | (-4,-1,2) | C. | (-4,1,2) | D. | (4,-1,-2) |
1.各顶点都在一个球面上的正四棱柱(底面是正方形,侧棱垂直于底面)高为2,体积为8,则这个球的表面积是( )
| A. | 16π | B. | 12π | C. | 10π | D. | 8π |
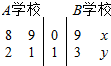 以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.
以下茎叶图记录了在高三一诊模拟考试中,A,B两个学校的各4个班的优生人数,其中有两个数据模糊不清,在图中用x,y表示,统计显示,A,B两个学校的优生人数的平均值相等,A校优生人数的方差比B校优生人数的方差小1.