题目内容
13.已知三角形的顶点为A(0,2)、B(-3,1)、C(-3,4),求三角形三边所在的直线的方程.分析 利用点斜式方程能求出△ABC三边所在的直线方程.
解答 解:KAB=$\frac{2-1}{0-(-3)}$=$\frac{1}{3}$,
直线AB的方程是:y-1=$\frac{1}{3}$(x+3),
即x-3y+6=0;
KBC不存在,BC方程是x=-3,
KAC=$\frac{2-4}{0-(-3)}$=-$\frac{2}{3}$,
直线AC的方程是:y-4=-$\frac{2}{3}$(x+3),
即2x+3y-6=0.
点评 本题考查直线方程的求法,解题时要认真审题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C的半径R取值范围是( )
| A. | (0,2) | B. | (0,$\sqrt{5}$) | C. | (0,2$\sqrt{5}$) | D. | (0,10) |
18.不等式($\frac{1}{2}$-x)($\frac{1}{3}$+x)>0的解集为( )
| A. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x<-$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|x<-$\frac{1}{2}$或x>$\frac{1}{3}$} |
2.曲线y=$\frac{1}{2}$x2-2x在x=3处的切线的倾斜角为( )
| A. | 45° | B. | -45° | C. | 135° | D. | -135° |
1.已知a,b为异面直线,下列结论不正确的是( )
| A. | 必存在平面α使得a∥α,b∥α | |
| B. | 必存在平面α使得a,b与α所成角相等 | |
| C. | 必存在平面α使得a?α,b⊥α | |
| D. | 必存在平面α使得a,b与α的距离相等 |
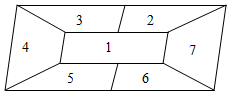 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种. 如图所示,某地有南北街道5条,东西街道6条,一邮电员从该地东北角的邮局A出发,送信到西南角的B地,且经过C地,要求所走的路程最短,共有多少种不同的走法?
如图所示,某地有南北街道5条,东西街道6条,一邮电员从该地东北角的邮局A出发,送信到西南角的B地,且经过C地,要求所走的路程最短,共有多少种不同的走法?