题目内容
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(1)求曲线E的方程;
(2)过点A且倾斜角是45°的直线l交曲线E于两点H、Q,求|HQ|.
解:(1)∵![]() =2
=2![]() ,
,![]() ·
·![]() =0,
=0,
∴NP为AM的垂直平分线.∴|NA|=|NM|.
又∵|CN|+|NM|=2![]() ,∴|CN|+|AN|=2
,∴|CN|+|AN|=2![]() >2.
>2.
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆,
且椭圆长轴长为2a=2![]() ,焦距2c=2.∴a=
,焦距2c=2.∴a=![]() ,c=1,b2=1.
,c=1,b2=1.
∴曲线E的方程为![]() +y2=1.
+y2=1.
(2)直线l的斜率k=tan45°=1,
∴直线l的方程为y=x-1.
由 消去y得3x2-4x=0.
消去y得3x2-4x=0.
设H(x1,y1),Q(x2,y2),则x1+x2=![]() ,x1x2=0,
,x1x2=0,
∴|HQ|=![]() |x1-x2|=
|x1-x2|=![]() ·
·![]() =
=![]() ·(
·(![]() )2=
)2=![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
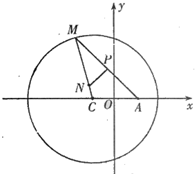 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
A、
| ||
B、
| ||
C、x2+
| ||
D、x2-
|
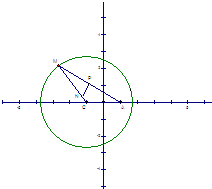 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足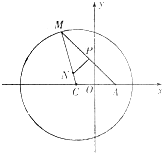 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E. (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足