题目内容
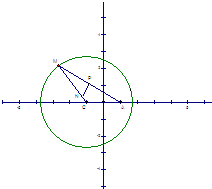 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足| AM |
| AP |
| NP |
| AM |
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),且满足
| FG |
| FH |
分析:(1)利用线段垂直平分线的性质推出 NC+NM=r=2
>AC,再利用椭圆的定义知,点N的轨迹是以A、C 为焦点的椭圆,利用待定系数法求出椭圆的方程
(2)不妨设FH斜率为k,且将原点移至F,则直线FH方程为y=kx,则椭圆方程变为
+(y-2)2=1,将直线与椭圆方程联立得(1+2k2)x2-8kx+6=0,结合题设条件求参数λ的范围
| 2 |
(2)不妨设FH斜率为k,且将原点移至F,则直线FH方程为y=kx,则椭圆方程变为
| x2 |
| 2 |
解答:解:(1)设点N的坐标为(x,y),
∵
=2
,∴点P为AM的中点,
∵
•
=0,∴NP⊥AM,∴NP是线段AM的垂直平分线,∴NM=NA,
又点N在CM上,设圆的半径是 r,则 r=2
,
∴NC=r-NM,∴NC+NM=r=2
>AC,
∴点N的轨迹是以A、C 为焦点的椭圆,
∴2a=2
,c=1,可求得b=1,
∴椭圆
+y2=1,即曲线E的方程:
+y2=1.
(2)当斜率不存在时,直线与曲线E有2个交点此时参数的值为λ=
,
不妨设FH斜率为k,且将原点移至F,
则直线FH方程为y=kx,椭圆方程变为
+(y-2)2=1,
将直线方程代入椭圆得
+(kx-2)2=1,整理得(1+2k2)x2-8kx+6=0,
直线与曲线E有二不同的交点,故△=(-8k)2-4•6(1+2k2)=16k2-24>0,即k2>
,
因为左右对称,可以研究单侧,
当k>0时,λ=
=
即λ=
=
由k2>
,即0<
<1,即0<
<1,
令t=
∈(0,1),则λ=
,t∈(0,1),
由于λ=
=
-1,故函数在t∈(0,1)上是减函数,故
<λ<1
综上,参数的取值范围是
≤λ<1
∵
| AM |
| AP |
∵
| NP |
| AM |
又点N在CM上,设圆的半径是 r,则 r=2
| 2 |
∴NC=r-NM,∴NC+NM=r=2
| 2 |
∴点N的轨迹是以A、C 为焦点的椭圆,
∴2a=2
| 2 |
∴椭圆
| x2 |
| 2 |
| x2 |
| 2 |
(2)当斜率不存在时,直线与曲线E有2个交点此时参数的值为λ=
| 1 |
| 3 |
不妨设FH斜率为k,且将原点移至F,
则直线FH方程为y=kx,椭圆方程变为
| x2 |
| 2 |
将直线方程代入椭圆得
| x2 |
| 2 |
直线与曲线E有二不同的交点,故△=(-8k)2-4•6(1+2k2)=16k2-24>0,即k2>
| 3 |
| 2 |
因为左右对称,可以研究单侧,
当k>0时,λ=
| x1 |
| x2 |
-b-
| ||
-b+
|
8k-
| ||
8k+
|
2-
| ||||
2+
|
由k2>
| 3 |
| 2 |
| 3 |
| 2k2 |
1-
|
令t=
1-
|
| 2-t |
| 2+t |
由于λ=
| 2-t |
| 2+t |
| 4 |
| 2+t |
| 1 |
| 3 |
综上,参数的取值范围是
| 1 |
| 3 |
点评:本题考查直线与圆锥曲线的综合题,解题的关键是掌握圆锥曲线的定义,由题设条件判断出所求的轨迹是椭圆,以及能将求两线段比值的问题转化为坐标比值,以利于用直线与圆锥曲线的方程研究参数的取值范围,本题解题过程中把曲线中心移到点(0,2),重新建系,使得椭圆方程得以简化且给后续解题带来了极大的方便,使问题转化为在k>0上求参数的范围,解题时要注意此类技巧的使用.本题综合性强运算较繁杂,做题时要严谨认真.

练习册系列答案
相关题目
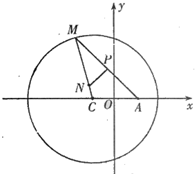 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
A、
| ||
B、
| ||
C、x2+
| ||
D、x2-
|
 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足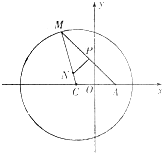 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E.
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足AM=2AP,NP⊥AM,点N的轨迹为曲线E. (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足