题目内容
某市用37辆汽车往灾区运送一批救灾物资，假设以v（km/h）的速度直达灾区，已知某市到灾区公路线长400km，为了安全起见，两辆汽车的间距不得小于(
)2km，那么这批物资全部到达灾区的最少时间是 h（车身长度不计）．
| v |
| 20 |
考点：函数模型的选择与应用
专题：函数的性质及应用
分析：由题意可知，t相当于：最后一辆车行驶了36个(
)2km+400km所用的时间，利用基本不等式，即可得出结论．
| v |
| 20 |
解答：
解：设全部物资到达灾区所需时间为t小时，
由题意可知，t相当于：最后一辆车行驶了36个(
)2km+400km所用的时间，
因此，t=
≥12．
当且仅当
=
，即v=
时取“=”．
故这些汽车以
km/h的速度匀速行驶时，所需时间最少要12小时．
故答案为：12．
由题意可知，t相当于：最后一辆车行驶了36个(
| v |
| 20 |
因此，t=
36×(
| ||
| v |
当且仅当
| 36v |
| 400 |
| 400 |
| v |
| 200 |
| 3 |
故这些汽车以
| 200 |
| 3 |
故答案为：12．
点评：本题考查基本不等式在最值问题中的应用，考查利用数学知识解决实际问题，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
设点P在曲线y=x2上，点Q在直线y=2x-2上，则PQ的最小值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
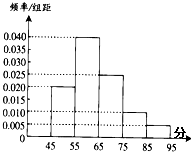为了调查某班学生做数学题的基本能力，随机抽查了部分学生某次做一份满分为100分的数学试题，他们所得分数的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图如图，则这些学生的平均分为
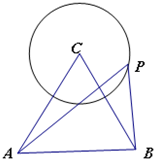如图，△ABC是边长为2