题目内容
9.求下列函数的值域:(1)y=log2(x2+8);
(2)y=25x-5x+1+6.
分析 (1)由真数的范围结合对数函数的单调性求得函数y=log2(x2+8)的值域;
(2)令t=5x(t>0)换元,然后利用配方法求得答案.
解答 解:(1)∵x2+8≥8,
∴log2(x2+8)≥log28=3,
故函数y=log2(x2+8)的值域为[3,+∞);
(2)y=25x-5x+1+6=(5x)2-5•5x+6,
令t=5x(t>0),
则原函数化为g(t)=${t}^{2}-5t+6=(t-\frac{5}{2})^{2}-\frac{1}{4}$.
∴当t=$\frac{5}{2}$时,$g(t)_{min}=-\frac{1}{4}$;
即y=25x-5x+1+6的最小值为$-\frac{1}{4}$,
则函数y=25x-5x+1+6的值域为[-$\frac{1}{4}$,+∞).
点评 本题考查函数的值域及其求法,考查了换元法,训练了利用配方法求二次函数的值域,是基础题.

练习册系列答案
相关题目
4.函数y=3${\;}^{ax-{x}^{2}}$在区间(1,+∞)上单调递减,则实数a的取值范围是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,2] | D. | [2,+∞) |
18.已知抛物线y=2x2+ax-1的顶点坐标为(1,b),则( )
| A. | a<4,b=3 | B. | a=-4,b=3 | C. | a=4,b=-3 | D. | a=-4,b=-3 |
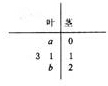 如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.
如图所示是某组数据的茎叶图,已知该组数据的平均数为$\frac{23}{2}$,ab=1(a,b∈R),则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$.