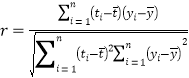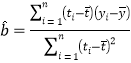题目内容
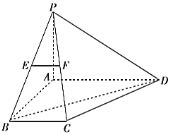
【题目】如图所示的几何体B-ACDE中,AB⊥AC,AB=4,AC=3,DC⊥平面ABC,EA⊥平面ABC,点M在线段BC上,且AM=![]() .
.
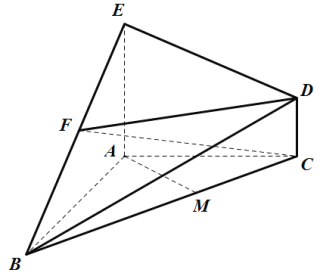
(1)证明:AM⊥平面BCD;
(2)若点F为线段BE的中点,且三棱锥F-BCD的体积为1,求CD的长度.
【答案】(1)证明见解析(2)![]()
【解析】
(1)证明![]() ,根据余弦定理得到
,根据余弦定理得到![]() ,再根据勾股定理得到
,再根据勾股定理得到![]() ,得到证明.
,得到证明.
(2))取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() 平面
平面![]() ,故点
,故点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,设
的距离,设![]() ,根据体积得到答案.
,根据体积得到答案.
(1)![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
由![]() 得
得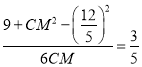 ,
,![]()
![]() .
.
![]()
![]() ,
,![]() ,即
,即![]() .
.
![]()
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
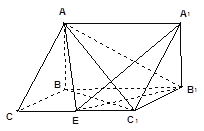
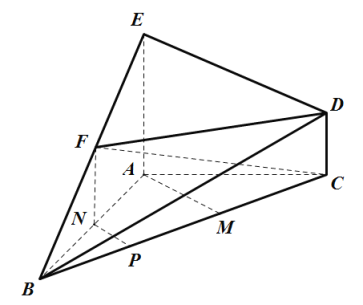
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() 点
点![]() 为线段
为线段![]() 中点,
中点,![]()
![]() .
.
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() ,
,![]() ,
,![]()
![]() .
.
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
![]() 点
点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
设![]() ,则
,则![]() ,
,![]()
![]() ,即
,即![]() 长为
长为![]() .
.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】为了迎接2019年的高考,某学校进行了第一次模拟考试,其中五个班的考试成绩在500分以上的人数如下表,![]() 为班级,
为班级,![]() 表示500分以上的人数
表示500分以上的人数
| 1 | 2 | 3 | 4 | 5 |
| 20 | 25 | 30 | 30 | 25 |
(1)若给出数据,班级![]() 与考试成绩500以上的人数
与考试成绩500以上的人数![]() ,满足回归直线方程
,满足回归直线方程![]() ,求出该回归直线方程;
,求出该回归直线方程;
(2)学校为了更好的提高学生的成绩,了解一模的考试成绩,从考试成绩在500分以上1,3班学生中,利用分层抽样抽取5人进行调研,再从选中的5人中,再选3名学生写出“经验介绍”文章,则选的三名学生1班一名,3班2名的概率.
参考公式: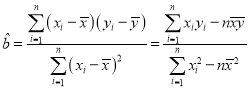 ,
,![]() .
.