题目内容
已知函数f(x)=x2-2ax,求:
(1)当a=1时,在区间[0,3]上的最小值;
(2)在区间[-1,1]上的最小值.
(1)当a=1时,在区间[0,3]上的最小值;
(2)在区间[-1,1]上的最小值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)当a=1时,函数f(x)=x2-2x=(x-1)2-1,利用二次函数的性质求得函数在区间[0,3]上的最小值.
(2)函数f(x)=x2-2ax的图象的对称轴方程为x=a,利用二次函数的性质,分类讨论求得函数在区间[-1,1]上的最小值.
(2)函数f(x)=x2-2ax的图象的对称轴方程为x=a,利用二次函数的性质,分类讨论求得函数在区间[-1,1]上的最小值.
解答:
解:(1)当a=1时,函数f(x)=x2-2x=(x-1)2-1,在区间[0,3]上,当x=1时,函数取得最小值为-1.
(2)函数f(x)=x2-2ax的图象的对称轴方程为x=a,当a<-1时,函数在区间[-1,1]上单调递增,最小值为f(-1)=1+2a;
当a∈[-1,1]时,函数在区间[-1,1]上的最小值为f(a)=-a2;
当a>1时,函数在区间[-1,1]上单调递减,最小值为f(1)=1-2a.
(2)函数f(x)=x2-2ax的图象的对称轴方程为x=a,当a<-1时,函数在区间[-1,1]上单调递增,最小值为f(-1)=1+2a;
当a∈[-1,1]时,函数在区间[-1,1]上的最小值为f(a)=-a2;
当a>1时,函数在区间[-1,1]上单调递减,最小值为f(1)=1-2a.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属基础题.

练习册系列答案
相关题目
已知log7(2
-1)+log2(
+1)=a,则log7(2
+1)+log2(
-1)=( )
| 2 |
| 2 |
| 2 |
| 2 |
| A、1+a | B、1-a | C、a | D、-a |
设i是虚数单位,复数
( )
| 7+4i |
| 1+2i |
| A、3-2i | B、3+2i |
| C、2-3i | D、2+3i |
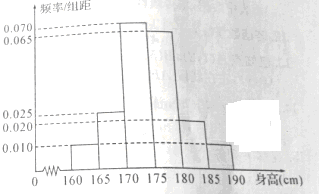 为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.
为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.