题目内容
设向量a=(4cosα,sinα),b=(sinβ,4cosβ),c=(cosβ,-4sinβ).
(1)若a与b-2c垂直,求tan(α+β)的值;
(2)求|b+c|的最大值;
(3)若tanαtanβ=16,求证:a∥b.
(1)由a与b-2c垂直.a·(b-2c)=a·b-2a·c=0,
即4sin(α+β)-8cos(α+β)=0,tan(α+β)=2.
(2)b+c=(sinβ+cosβ,4cosβ-4sinβ),
|b+c|2=sin2β+2sinβcosβ+cos2β+16cos2β-32cosβsinβ+16sin2β
=17-30sinβcosβ=17-15sin2β最大值为32,
∴|b+c|的最大值为4 .
.
(3)证明:由tanαtanβ=16得sinαsinβ=16cosαcosβ,
即4cosα·4cosβ-sinαsinβ=0,∴a∥b.

练习册系列答案
相关题目
 ,则点B的坐标为________.
,则点B的坐标为________.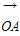 =a,
=a,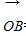 =tb,
=tb,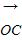 =
=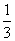 (a+b),那么当实数t为何值时,A、B、C三点共线?
(a+b),那么当实数t为何值时,A、B、C三点共线?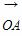 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),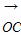 =(5-m,-3-m).
=(5-m,-3-m). ,则向量a与c的夹角为( )
,则向量a与c的夹角为( )
 D.
D. 
 =( )
=( ) (O为坐标原点)等于( )
(O为坐标原点)等于( )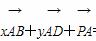 =0(x,y∈R),则当点P在以A为圆心,
=0(x,y∈R),则当点P在以A为圆心,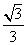 |
|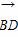 |为半径的圆上时,实数x,y应满足关系式为( )
|为半径的圆上时,实数x,y应满足关系式为( ) =
= ,那么
,那么 等于( )
等于( ) B.
B. C.
C. D.
D.