题目内容
在等边△ABC中,(1)求证:a⊥(b-c);
(2)解关于x的不等式|xa+b+c|>1.
(1)证明:∵△ABC为等边三角形,且![]() =a,
=a,![]() =b,
=b,![]() =c,|a|=2,
=c,|a|=2,
∴|a|=|b|=|c|=2,且a、b、c两两夹角均为120°.
故a·(b-c)=a·b-a·c=|a||b|cos120°-|a||c|cos120°=0.
∴a⊥(b-c).
(2)解:原不等式可化为|xa+b+c|2>1,
即a2x2+b2+c2+2(a·b+a·c)x+2b·c>1,
即4x2-8x+3>0.
解得x<![]() 或x>
或x>![]() .
.
∴原不等式的解集为{x|x<![]() 或x>
或x>![]() }.
}.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等边△ABC中,D是BC上的一点,若AB=4,BD=1,则
?
=( )
| AB |
| AD |
| A、14 | ||
| B、18 | ||
C、16-2
| ||
D、16+2
|
 如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
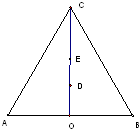 如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且
如图,在等边△ABC中,O为边AB的中点,AB=4,D、E为△ABC的高线上的点,且