题目内容
在等边△ABC中,D在AB上运动,E在AC上运动,DE∥BC,将△ADE沿DE折起,使二面角A-DE-B的平面角为600,当四棱锥A-DBCE体积最大时,AD:DB等于( )
分析:在原图中取DE的中点O,则在立体图中,可证明∠AOF是二面角A-DE-B的平面角,且可得平面AOF⊥平面BCDE,再作出等边△AOF的边OF的高AM,再证明AM是四棱锥A-BCED的高即可.
解答: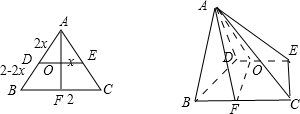 解:如图所示:设BC=2,AD=2x,BD=2-2x.(0<x<1).
解:如图所示:设BC=2,AD=2x,BD=2-2x.(0<x<1).
∵DE∥BC,∴△ADE是等边三角形,取DE的中点O,则DO=OE=x,AO=
x.
∴S四边形BCDE=S△ABC-S△ADE=
×22-
×(2x)2=
(1-x2).
由于O是等边△ADE的边DE的中点,∴AF⊥DE.∴在第二个图中,AO⊥DE,FO⊥DE.∴∠AOF是二面角A-DE-B的平面角.
∴∠AOF=60°.又AO=OF,∴△AOF是等边三角形.
过点A作AM⊥OF,M是垂足,得AM=
×
x=
x.
由DE⊥平面AOF,∴平面AOF⊥平面BCED,∴AM⊥平面BCED,∴AM是四棱锥的高.
∴V四棱锥A-BCED=
×
(1-x2)×
x=
×(x-x3),
∴V′=
(1-3x2),令V′=0,解得x=
(∵0<x<1).
∵当x∈(0,
)时,V′>0;当x∈(
,1)时,V′<0.
∴函数V在区间(0,
)上单调递增,在区间(
,1)上单调递减.所以函数V在x=
时取得最大值.
∴
=
=
=
=
.
故选B.
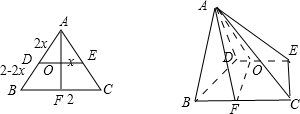 解:如图所示:设BC=2,AD=2x,BD=2-2x.(0<x<1).
解:如图所示:设BC=2,AD=2x,BD=2-2x.(0<x<1).∵DE∥BC,∴△ADE是等边三角形,取DE的中点O,则DO=OE=x,AO=
| 3 |
∴S四边形BCDE=S△ABC-S△ADE=
| ||
| 4 |
| ||
| 4 |
| 3 |
由于O是等边△ADE的边DE的中点,∴AF⊥DE.∴在第二个图中,AO⊥DE,FO⊥DE.∴∠AOF是二面角A-DE-B的平面角.
∴∠AOF=60°.又AO=OF,∴△AOF是等边三角形.
过点A作AM⊥OF,M是垂足,得AM=
| ||
| 2 |
| 3 |
| 3 |
| 2 |
由DE⊥平面AOF,∴平面AOF⊥平面BCED,∴AM⊥平面BCED,∴AM是四棱锥的高.
∴V四棱锥A-BCED=
| 1 |
| 3 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
∴V′=
| ||
| 2 |
| ||
| 3 |
∵当x∈(0,
| ||
| 3 |
| ||
| 3 |
∴函数V在区间(0,
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴
| AD |
| DB |
| 2x |
| 2-2x |
| x |
| 1-x |
| ||||
1-
|
| 1 | ||
|
故选B.
点评:本题考查了四棱锥的体积,作出二面角的平面角和求出四棱锥的高是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在等边△ABC中,D是BC上的一点,若AB=4,BD=1,则
?
=( )
| AB |
| AD |
| A、14 | ||
| B、18 | ||
C、16-2
| ||
D、16+2
|
 如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为
如图,在等边△ABC中,以AB为直径的⊙O与BC相交于点D,连接AD,则∠DAC的度数为