题目内容
在等边△ABC中，边长为2，D为边BC中点，点E在边AC上，且CE=2EA，则
•
的值为
| AD |
| BE |
-2
-2
．分析：以
，
为基向量，将
，
分别表示，利用向量数量积的运算法则，转化为
，
的运算．
| AB |
| AC |
| AD |
| BE |
| AB |
| AC |
解答：解：如图
以
，
为基向量，则
=
(
+
，
=
+
=
-
-
=
-
•
=
(
+
•(
-
=-
2-
•
+
2=
×4-
×2×2×cos60°+
×4=-2
故答案为：-2
以| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AC) |
| BE |
| BC |
| CE |
| AC |
| AB |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AC |
| AB |
| AD |
| BE |
| 1 |
| 2 |
| AB |
| AC) |
| 1 |
| 3 |
| AC |
| AB) |
| 1 |
| 2 |
| AB |
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 6 |
| AC |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
故答案为：-2
点评：本题考查了向量加减的几何意义，向量数量积的计算，直接利用定义不易求解，这里利用平面向量基本定理，进行转化计算．
练习册系列答案
相关题目
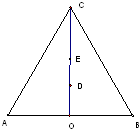如图，在等边△ABC中，O为边AB的中点，AB=4，D、E为△ABC的高线上的点，且