题目内容
已知:向量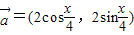 ,
,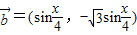 ,函数
,函数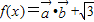
(1)求函数y=f(x)的最小正周期及最值;
(2)将函数y=f(x)的图象纵坐标不变,横坐标伸长为原来的2倍后,再向左平移
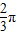 得到函数y=g(x),判断函数y=g(x)的奇偶性,并说明理由.
得到函数y=g(x),判断函数y=g(x)的奇偶性,并说明理由.
【答案】分析:(1)利用两个向量数量积公式、两角和差的正弦公式化简函数y=f(x)的解析式为2sin( +
+ ),由此求出它的最小正周期和最小值.
),由此求出它的最小正周期和最小值.
(2)第一次变换后得到y=2sin( +
+ )的图象,第二次变换后得到y=2cos
)的图象,第二次变换后得到y=2cos 的图象,再由偶函数的定义判断它为偶函数.
的图象,再由偶函数的定义判断它为偶函数.
解答:解:(1)∵函数y=f(x)= =sin
=sin -2
-2 
 +
+ =sin
=sin +
+ cos
cos =2sin(
=2sin( +
+ ),
),
故函数y=f(x)的最小正周期为 =4π,最小值为-2.
=4π,最小值为-2.
(2)将函数y=f(x)的图象纵坐标不变,横坐标伸长为原来的2倍后,得到函数y=2sin( +
+ )的图象,
)的图象,
再向左平移 得到函数y=2sin[
得到函数y=2sin[ +
+ ]=2sin(
]=2sin( +
+ )=2cos
)=2cos 的图象,
的图象,
故函数y=g(x)=2cos ,定义域为R,
,定义域为R,
因为g(-x)=2cos(- )=2 cos
)=2 cos =g(x),
=g(x),
故函数y=g(x)是偶函数.
点评:本题主要考查两角和差的正弦公式,诱导公式、两个向量数量积公式的应用,三角函数的周期性和求法、正弦函数的定义域和值域,函数y=Asin(ωx+∅)的图象变换,属于中档题.
 +
+ ),由此求出它的最小正周期和最小值.
),由此求出它的最小正周期和最小值.(2)第一次变换后得到y=2sin(
 +
+ )的图象,第二次变换后得到y=2cos
)的图象,第二次变换后得到y=2cos 的图象,再由偶函数的定义判断它为偶函数.
的图象,再由偶函数的定义判断它为偶函数.解答:解:(1)∵函数y=f(x)=
 =sin
=sin -2
-2 
 +
+ =sin
=sin +
+ cos
cos =2sin(
=2sin( +
+ ),
),故函数y=f(x)的最小正周期为
 =4π,最小值为-2.
=4π,最小值为-2.(2)将函数y=f(x)的图象纵坐标不变,横坐标伸长为原来的2倍后,得到函数y=2sin(
 +
+ )的图象,
)的图象,再向左平移
 得到函数y=2sin[
得到函数y=2sin[ +
+ ]=2sin(
]=2sin( +
+ )=2cos
)=2cos 的图象,
的图象,故函数y=g(x)=2cos
 ,定义域为R,
,定义域为R,因为g(-x)=2cos(-
 )=2 cos
)=2 cos =g(x),
=g(x),故函数y=g(x)是偶函数.
点评:本题主要考查两角和差的正弦公式,诱导公式、两个向量数量积公式的应用,三角函数的周期性和求法、正弦函数的定义域和值域,函数y=Asin(ωx+∅)的图象变换,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
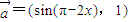 ,
,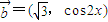 ,函数
,函数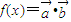 .
.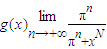 (0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标.
(0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标. ,
,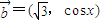 ,函数
,函数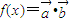 .
.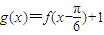 ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标. ,
, ,函数
,函数 .
. ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.