题目内容
已知平面向量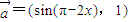 ,
,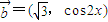 ,函数
,函数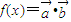 .
.(1)写出函数f(x)的单调递减区间;
(2)设
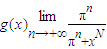 (0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标.
(0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标.
【答案】分析:(1)用向量的数量积的坐标运算求出f(x)的解析式,整体代换的方法求出单调区间
(2)用极限的运算法则求出g(x)为分段函数,再解三角方程得交点坐标.
解答:[理科]解:(1) ,
,
单调递减区间为[ ](k∈z);
](k∈z);
(2)g(x)=
当0<x<π时,解2sin(2x+ )=1,得x=
)=1,得x= ,
,
当x=π时,解2sin(2x+ )=
)= ,无解,(11分)
,无解,(11分)
当π<x<2π时,解2sin(2x+ )=0,得x=
)=0,得x= ,
,
所以交点坐标为:( ),(
),( ,0).
,0).
点评:考查向量的数量积,极限的运算法则,三角函数的单调区间及三角方程的解法.
(2)用极限的运算法则求出g(x)为分段函数,再解三角方程得交点坐标.
解答:[理科]解:(1)
 ,
,单调递减区间为[
 ](k∈z);
](k∈z);(2)g(x)=

当0<x<π时,解2sin(2x+
 )=1,得x=
)=1,得x= ,
,当x=π时,解2sin(2x+
 )=
)= ,无解,(11分)
,无解,(11分)当π<x<2π时,解2sin(2x+
 )=0,得x=
)=0,得x= ,
,所以交点坐标为:(
 ),(
),( ,0).
,0).点评:考查向量的数量积,极限的运算法则,三角函数的单调区间及三角方程的解法.

练习册系列答案
相关题目
 ,
, ,函数
,函数 .
. ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标. ,
,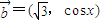 ,函数
,函数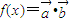 .
.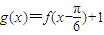 ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标. ,
, ,函数
,函数 .
. ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标. ,
, ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; ,求直线
,求直线 与
与 在闭区间
在闭区间 上的图像的所有交点坐标.
上的图像的所有交点坐标.