题目内容
已知平面向量 ,
,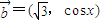 ,函数
,函数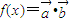 .
.(1)写出函数f(x)的单调递减区间;
(2)设
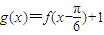 ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
【答案】分析:(1)求函数f(x)的单调递减区间要先确定函数f(x)的解析式,根据解析式再求单调区间.
(2)由(1)中函数f(x)的解析式,不难给出函数g(x)的解析式,而两个函数图象的交点,即是求由两个解析式联立的方程组.
解答:解:(1)函数 =
=
∴函数的单调递减区间为
(2)g(x)=f(x- )+1=2sinx+1
)+1=2sinx+1
解g(x)=2,即sinx= ,x∈[0,π]得:
,x∈[0,π]得:
x= 或x=
或x=
所以交点坐标为:
点评:本题主要的考查点是正弦函数的单调性,解题的切入点是根据平面向量的数量积运算给出函数f(x)的解析式,而(2)中求函数图象交点的坐标,则可转化为解方程的问题进行求解.
(2)由(1)中函数f(x)的解析式,不难给出函数g(x)的解析式,而两个函数图象的交点,即是求由两个解析式联立的方程组.
解答:解:(1)函数
 =
=
∴函数的单调递减区间为

(2)g(x)=f(x-
 )+1=2sinx+1
)+1=2sinx+1解g(x)=2,即sinx=
 ,x∈[0,π]得:
,x∈[0,π]得:x=
 或x=
或x=
所以交点坐标为:

点评:本题主要的考查点是正弦函数的单调性,解题的切入点是根据平面向量的数量积运算给出函数f(x)的解析式,而(2)中求函数图象交点的坐标,则可转化为解方程的问题进行求解.

练习册系列答案
相关题目
 ,
, ,函数
,函数 .
. ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.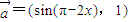 ,
,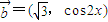 ,函数
,函数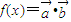 .
.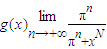 (0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标.
(0<x<2π),求函数y=f(x)与y=g(x)图象的所有交点坐标. ,
, ,函数
,函数 .
. ,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标.
,求直线y=2与y=g(x)在闭区间[0,π]上的图象的所有交点坐标. ,
, ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; ,求直线
,求直线 与
与 在闭区间
在闭区间 上的图像的所有交点坐标.
上的图像的所有交点坐标.