题目内容
已知函数 ,其中
,其中 是常数且
是常数且 .
.
(1)当 时,
时, 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(2)当 时,讨论
时,讨论 的单调性;
的单调性;
(3)设 是正整数,证明:
是正整数,证明: .
.
 ,其中
,其中 是常数且
是常数且 .
.(1)当
 时,
时, 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;(2)当
 时,讨论
时,讨论 的单调性;
的单调性;(3)设
 是正整数,证明:
是正整数,证明: .
.(1)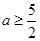 ;(2)当
;(2)当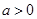 时,
时,  的减区间为
的减区间为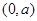 ,增区间为
,增区间为 ;当
;当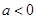 时,
时,  的减区间为
的减区间为 ,增区间为
,增区间为 ;(3)详见解析.
;(3)详见解析.
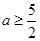 ;(2)当
;(2)当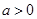 时,
时,  的减区间为
的减区间为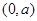 ,增区间为
,增区间为 ;当
;当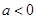 时,
时,  的减区间为
的减区间为 ,增区间为
,增区间为 ;(3)详见解析.
;(3)详见解析.试题分析:(1)利用导数法,然后才有分离参数的思路进行求解; (2)明确函数的解析式,利用求导法和分类讨论进行求解;(3)用
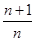 代替
代替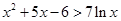 中的
中的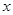 得到
得到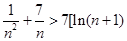
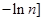 ,再证明不等式成立.
,再证明不等式成立.试题解析:(1)∵
 ,则
,则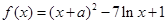 ,∴
,∴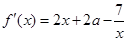 ,
,∵当
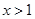 时,
时, 是增函数,∴
是增函数,∴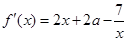 在
在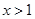 时恒成立. (2分)
时恒成立. (2分)即
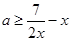 在
在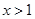 时恒成立. ∵当
时恒成立. ∵当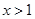 时,
时,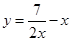 是减函数,
是减函数,∴当
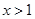 时,
时, ,∴
,∴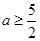 . (4分)
. (4分)(2)∵
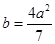 ,∴
,∴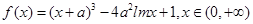 ,
,∴
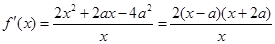 , (5分)
, (5分)∴当
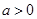 时,由
时,由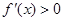 得
得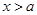 或
或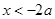 ,故
,故 的减区间为
的减区间为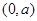 ,增区间为
,增区间为 .
.当
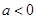 时,由
时,由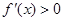 得
得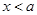 或
或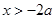 ,故
,故 的减区间为
的减区间为 ,增区间为
,增区间为 . (9分)
. (9分)(3)由(1)知,当
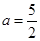 ,
, 时,
时,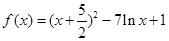 在
在 时增函数,
时增函数,∴
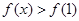 ,即
,即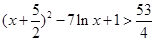 ,∴
,∴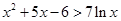 ,
,∵
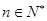 ,∴
,∴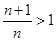 ,∴
,∴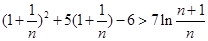 ,
,即
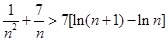 , (12分)
, (12分)∴
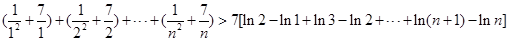
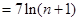
∴
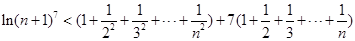 . (14分)
. (14分)
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
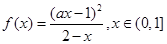 ,它的一个极值点是
,它的一个极值点是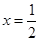 .
.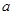 的值及
的值及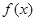 的值域;
的值域;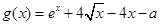 ,试求函数
,试求函数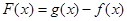 的零点的个数.
的零点的个数. 为函数
为函数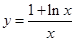 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线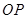 的斜率
的斜率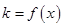 .
.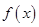 在区间
在区间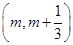
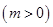 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;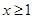 时,不等式
时,不等式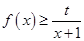 恒成立,求实数
恒成立,求实数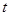 的取值范围;
的取值范围;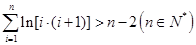 .
.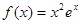 ,当曲线y = f(x)的切线L的斜率为正数时,L在x轴上截距的取值范围为 .
,当曲线y = f(x)的切线L的斜率为正数时,L在x轴上截距的取值范围为 . 在
在 处有极小值,则实数
处有极小值,则实数 .
.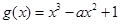 在区间
在区间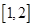 上是单调递减函数,则实数
上是单调递减函数,则实数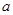 的取值范围是 .
的取值范围是 .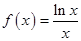 的单调递增区间是 .
的单调递增区间是 . 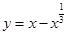 的图象大致为( )
的图象大致为( )
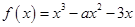
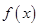 在
在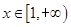 上是增函数,求实数
上是增函数,求实数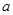 的取值范围;
的取值范围;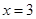 是
是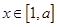 上的最小值和最大值.
上的最小值和最大值.