题目内容
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15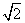 n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40 n mile处的B岛出发,朝北偏东θ
n mile/h,在甲船从A岛出发的同时,乙船从A岛正南40 n mile处的B岛出发,朝北偏东θ 的方向作匀速直线航行,速度为m n mile/h.
的方向作匀速直线航行,速度为m n mile/h.
(1)若两船能相遇,求m.
(2)当m=10 时,求两船出发后多长时间距离最近,最近距离为多少n mile?
时,求两船出发后多长时间距离最近,最近距离为多少n mile?

解析 (1)设t小时后,两船在M处相遇,
由tanθ= ,得sinθ=
,得sinθ= ,cosθ=
,cosθ= ,
,
所以sin∠AMB=sin(45°-θ)= .
.
由正弦定理, =
= ,∴AM=40
,∴AM=40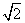 ,
,
同理得BM=40 .
.
∴t= =
= ,m=
,m= =15
=15 .
.

(2)以A为原点,BA所在直线为y轴建立如图所示的平面直角坐标系,设在t时刻甲、乙两船分别在P(x1,y1),Q(x2,y2)处,则|AP|=15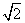 t,|BQ|=10
t,|BQ|=10 t.
t.

由任意角三角函数的定义,可得

即点P的坐标是(15t,15t),

即点Q的坐标是(10t,20t-40),
∴|PQ|= =
=
= ≥20
≥20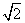 ,
,
当且仅当t=4时,|PQ|取得最小值20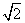 ,即两船出发4小时时,距离最近,最近距离为20
,即两船出发4小时时,距离最近,最近距离为20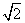 n mile.
n mile.

练习册系列答案
相关题目
 cos(x+θ)
cos(x+θ)  是偶函数,则θ的值为________.
是偶函数,则θ的值为________.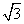 km,那么x的值为( ).
km,那么x的值为( ). 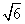 米,则旗杆的高度为________米.
米,则旗杆的高度为________米.
 =
=
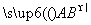 +
+
 ,则△ABM与△ABC的面积之比为________.
,则△ABM与△ABC的面积之比为________. ,记数列{an}的前n项之积为Πn,则Π2 011的值为( )
,记数列{an}的前n项之积为Πn,则Π2 011的值为( ) B.-1
B.-1