题目内容
10.在△ABC中,若$\overrightarrow{AB}$$•\overrightarrow{AC}$=7,|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=6,则△ABC的面积的最大值为12.分析 设A、B、C所对边分别为a,b,c,由$\overrightarrow{AB}$$•\overrightarrow{AC}$=7,|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=6,得bccosA=7,a=6①,由余弦定理可得b2+c2-2bccosA=36②,联立①②可得b2+c2=50,由不等式可得bc≤25,即可求出△ABC面积的最大值.
解答 解:设A、B、C所对边分别为a,b,c,由$\overrightarrow{AB}$$•\overrightarrow{AC}$=7,|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=6,得bccosA=7,a=6①,
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bc$\sqrt{1-co{s}^{2}A}$=$\frac{1}{2}bc\sqrt{1-\frac{49}{{b}^{2}{c}^{2}}}=\frac{1}{2}\sqrt{{b}^{2}{c}^{2}-49}$.
由余弦定理可得b2+c2-2bccosA=36②,
由①②消掉cosA得b2+c2=50,所以b2+c2≥2bc,
所以bc≤25,当且仅当b=c=5时取等号,
所以S△ABC=$\frac{1}{2}\sqrt{(bc)^{2}-49}$≤12,
故△ABC的面积的最大值为12,
故答案为:12.
点评 本题考查平面向量数量积的运算、三角形面积公式不等式求最值等知识,综合性较强,属于难题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.已知函数f(x)=|2x-2|+b的两个零点分别为x1,x2(x1>x2),则下列结论正确的是( )
| A. | 1<x1<2,x1+x2<2 | B. | 1<x1<2,x1+x2<1 | C. | x1>1,x1+x2<2 | D. | x1>1,x1+x2<1 |
19.双曲线上存在一点与其中心及一个焦点构成等边三角形,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{3}$+1 | C. | $\sqrt{3}$ | D. | $\sqrt{3}$-1 |
9.已知集合M={y|y=x2},用自然语言描述M应为( )
| A. | 函数y=x2的函数值组成的集合 | B. | 函数y=x2的自变量的值组成的集合 | ||
| C. | 函数y=x2的图象上的点组成的集合 | D. | 以上说法都不对 |
 如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.
如图,在△ABC中,CA=2,CB=1,CD是AB边上的中线.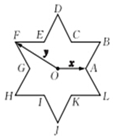 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.