题目内容
【题目】已知椭圆
的左右焦点分别为
，
，点
是椭圆
上一点，以
为直径的圆
：
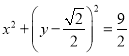过点.
（1）求椭圆的方程；
（2）过点且斜率大于0的直线
与的另一个交点为
，与直线
的交点为
，过点
且与垂直的直线
与直线交于点
，求
面积的最小值.
【答案】（1）
；（2）
.
【解析】
(1)先求出点
的坐标，再利用椭圆的定义求出
的值，即得椭圆方程；
(2)设
,
，将直线的方程代入椭圆方程求出
，进而表示出
的面积
，再利用基本不等式求出最小值.
解：(1)在圆
的方程中，令
，得到：
，
所以
，
，
又因为
且
，所以点坐标为
，
所以
，则
，
，
因此椭圆的方程为；
(2)设直线
：
，
所以点
的坐标为
，
设，，将直线代入椭圆方程得：
，
所以
，所以
，
直线
的方程为
，所以点
坐标为
，
所以
，
当且仅当
，即
时取等号，
综上，面积的最小值.
举一反三单元同步过关卷系列答案
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式，某市通过随机询问100名居民（男女居民各50名）喜欢支付宝支付还是微信支付，得到如下的
列联表：
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式：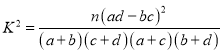
，
.
P（ | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是（ ）
A.有
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过
的前提下，认为“支付方式与性别有关”
C.在犯错误的概率不超过的前提下，认为“支付方式与性别有关”
D.有
以上的把握认为“支付方式与性别无关”
【题目】这次新冠肺炎疫情，是新中国成立以来在我国发生的传播速度最快、感染范围最广、防控难度最大的一次重大突发公共卫生事件.中华民族历史上经历过很多磨难，但从来没有被压垮过，而是愈挫愈勇，不断在磨难中成长，从磨难中奋起.在这次疫情中，全国人民展现出既有责任担当之勇、又有科学防控之智.某校高三学生也展开了对这次疫情的研究，一名同学在数据统计中发现，从2020年2月1日至2月7日期间，日期
和全国累计报告确诊病例数量
（单位：万人）之间的关系如下表：
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
全国累计报告确诊病例数量 | 1.4 | 1.7 | 2.0 | 2.4 | 2.8 | 3.1 | 3.5 |
（1）根据表中的数据，运用相关系数进行分析说明，是否可以用线性回归模型拟合与的关系？
（2）求出关于的线性回归方程
（系数精确到0.01）.并预测2月10日全国累计报告确诊病例数.
参考数据：
，
，
，
.
参考公式：相关系数
回归方程
中斜率和截距的最小二乘估计公式分别为：
，
.