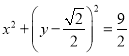题目内容
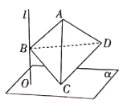
【题目】已知圆![]() ,定点
,定点![]() ,
,![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程
的方程
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,已知点
两点,已知点![]() ,直线
,直线![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 是否在定直线上,若存在,求出该直线方程;若不是,说明理由.
是否在定直线上,若存在,求出该直线方程;若不是,说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)设以![]() 为直径的圆心为
为直径的圆心为![]() ,切点为
,切点为![]() ,取
,取![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,计算得到
,计算得到![]() ,故轨迹为椭圆,计算得到答案.
,故轨迹为椭圆,计算得到答案.
(2)设直线的方程为![]() ,设
,设![]() ,联立方程得到
,联立方程得到
![]() ,
,![]() ,计算
,计算![]() ,得到答案.
,得到答案.
(1)设以![]() 为直径的圆心为
为直径的圆心为![]() ,切点为
,切点为![]() ,则
,则![]() ,
,
取![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,故
,故![]() ,
,
所以点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴为4的椭圆,其中
为焦点,长轴为4的椭圆,其中![]() ,
,
曲线方程为![]() .
.
(2)设直线的方程为![]() ,设
,设![]() ,
,
直线![]() 的方程为
的方程为![]() ,同理
,同理![]() ,
,
所以![]() ,
,
即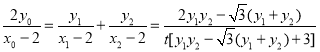 ,
,
联立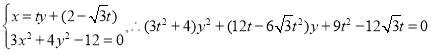 ,
,
所以![]() ,
,
代入得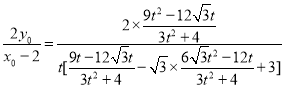
![]() ,
,
所以点![]() 都在定直线
都在定直线![]() 上.
上.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目