题目内容
求下列函数的单调区间:(1)y=x4-2x2+6;(2)y=-lnx+2x2.
思路分析:求出导数y′,分别令y′>0或y′<0.解出x的取值范围.便可得出单调区间.?
解:(1)y′=4x3-4x令y′>0,即4x3-4x>0解得-1<x<0或x>1.所以单调增区间为(-1,0)和(1,+∞).?
令y′<0,解得x<-1或0<x<1.因此单调减区间为(-∞,-1)和(0,1).?
(2)y′=4x-![]() ,令y′>0,即4x-
,令y′>0,即4x-![]() >0.解得-
>0.解得-![]() <x<0或x>
<x<0或x>![]() .令y′<0,即4x-
.令y′<0,即4x-![]() <0,解得x<-
<0,解得x<-![]() 或0<x<
或0<x<![]() .
.
∵定义域为x>0,∴单调增区间为(![]() ,+∞),单调减区间为(0,
,+∞),单调减区间为(0, ![]() ).
).
温馨提示
在求单调区间时,一定要在定义域内考虑.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;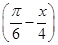 .
.