题目内容
△ABC中,下列说法正确的是( )
| A、asinA=bsinB |
| B、若a2+b2=c2,则△ABC为锐角三角形 |
| C、若A>B,则cosA<cosB |
| D、若sinB+sinC=sin2A,则b+c=a2 |
考点:正弦定理
专题:三角函数的图像与性质,解三角形
分析:根据正弦定理化简A,D中的条件,可以判定其错误,利用勾股定理可判断B错误,根据余弦函数性质可判断C正确.
解答:
解:对于A,根据正弦定理知,
a=2RsinA,b=2RsinB,
代入asinA=bsinB得,sin2A=sin2B,
显然A不成立;
对于B根据勾股定理可知,
若a2+b2=c2,则△ABC为直角三角形
易知B错误;.
对于C,根据余弦函数的单调性可知
若A>B,则cosA<cosB.
∴C正确;
对于D,根据正弦定理知,
sinB+sinC=sin2A可化为
2RsinB+2RsinC=2Rsin2A,
即b+c=asinA,
显然D不正确.
故选:C.
a=2RsinA,b=2RsinB,
代入asinA=bsinB得,sin2A=sin2B,
显然A不成立;
对于B根据勾股定理可知,
若a2+b2=c2,则△ABC为直角三角形
易知B错误;.
对于C,根据余弦函数的单调性可知
若A>B,则cosA<cosB.
∴C正确;
对于D,根据正弦定理知,
sinB+sinC=sin2A可化为
2RsinB+2RsinC=2Rsin2A,
即b+c=asinA,
显然D不正确.
故选:C.
点评:本题主要考查正弦定理,三角形内角和定理,勾股定理和余弦函数的单调性等知识的综合应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若复数i满足z(1+i)=2i,则在复平面内z对应的点的坐标是( )
| A、(1,1) |
| B、(1,-1) |
| C、(-1,1) |
| D、(-1,-1) |
在复平面内,复数z=
对应的点在( )
| 1-i |
| 1+2i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
f(x)是定义域为R的奇函数,且当x≥0时,f(x)=x(x-2);若关于x的方程f2(x)-f(x)+t=0的方程有6个不相等的实根,求实数t的取值范围( )
A、(0,
| ||
B、(-∞,
| ||
C、(-2,
| ||
| D、(-2,+∞) |
若A(-2,3)、B(3,-2)、C(
,m﹚三点在同一直线上,则m的值为( )
| 1 |
| 2 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
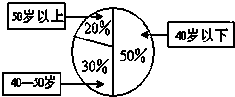 某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )