题目内容
证明:
+
=1-sinαcosα.
| sin3α |
| sinα+cosα |
| cos2α |
| 1+tanα |
考点:三角函数恒等式的证明
专题:三角函数的求值
分析:通过切化弦通分,利用立方差公式化简证明即可.
解答:
证明:
+
=
+
=
=
=1-sinαcosα.
所以等式成立.
| sin3α |
| sinα+cosα |
| cos2α |
| 1+tanα |
| sin3α |
| sinα+cosα |
| cos2α | ||
1+
|
| sin3α+cos2α |
| sinα+cosα |
=
| (sinα+cosα)(sin2α-sinα•cosα+cos2α) |
| sinα+cosα |
=1-sinαcosα.
所以等式成立.
点评:本题考查三角函数恒等式的证明,切化弦以及立方差公式的应用,考查计算能力.

练习册系列答案
相关题目
若正n边形的两条对角线都与直线l垂直,则直线l一定垂直于这个正n边形所在的平面,则n的取值可能是( )
| A、8 | B、7 | C、6 | D、5 |
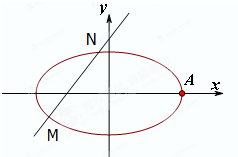 如图,已知点A是椭圆
如图,已知点A是椭圆