题目内容
1.已知平面内两点A(4,0),B(0,2)(1)求过P(2,3)点且与直线AB平行的直线l的方程;
(2)设O(0,0),求△OAB外接圆方程.
分析 (1)求出直线的斜率,利用点斜式求出直线方程;
(2)根据题意,△AOB是以AB为斜边的直角三角形,因此外接圆是以AB为直径的圆.由此算出AB中点C的坐标和AB长度,结合圆的标准方程形式,即可求出△AOB的外接圆的方程.
解答 解:(1)由已知得${k_{AB}}=\frac{2-0}{0-4}=-\frac{1}{2}$.
由点斜式$y-3=-\frac{1}{2}(x-2)$
∴直线l的方程x+2y-8=0.
(2)OA⊥OB,可得△AOB的外接圆是以AB为直径的圆
∵AB中点为C(2,1),|AB|=2$\sqrt{5}$.∴圆的圆心为C(2,1),半径为r=$\sqrt{5}$.
可得△AOB的外接圆的方程为(x-2)2+(y-1)2=5.
点评 本题着重考查了直线方程,考查圆的方程、中点坐标公式和三角形形状的判断等知识,属于基础题.

练习册系列答案
相关题目
6.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为80秒.若一名行人来到该路口遇到红灯,则至少需要等待30秒才出现绿灯的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{5}$ |
9.函数$f(x)=\frac{x^3}{3}+\frac{1}{x}$的导数f'(x)=( )
| A. | $\frac{x^2}{3}+\frac{1}{x}$ | B. | ${x^2}-\frac{1}{x^2}$ | C. | $-{x^2}-\frac{1}{x^2}$ | D. | x2+lnx |
16.某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
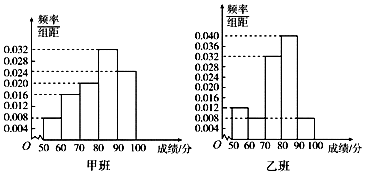
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.

(Ⅰ)根据频率分布直方图填写下面2×2列联表;
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
10.从1,2,3,4中任取两个数,记作a,b,则两数之和a+b小于5的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
11.某市5年中的煤气消耗量与使用煤气户数的历史资料如下:
(1)检验是否线性相关;
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
| 年份 | 2006 | 2007 | 2008 | 2009 | 2010 |
| x用户(万户) | 1 | 1.1 | 1.5 | 1.6 | 1.8 |
| y(万立方米) | 6 | 7 | 9 | 11 | 12 |
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?