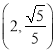题目内容
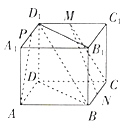
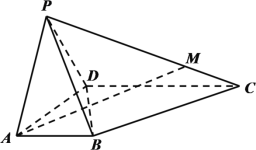
【题目】在梯形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 是等腰直角三角形,其中
是等腰直角三角形,其中![]() 为斜边,若把
为斜边,若把![]() 沿
沿![]() 边折叠到
边折叠到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
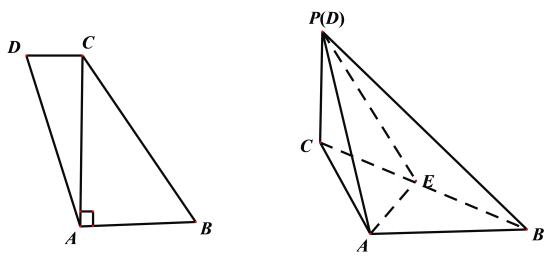
(1)证明:![]() .
.
(2)若![]() 为棱
为棱![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
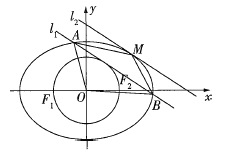
【答案】(1)见解析(2)![]()
【解析】
(1)由面面垂直,可知![]() 平面
平面![]() ,进而可证
,进而可证![]() .
.
(2)![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 轴的正方向,过点
轴的正方向,过点![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,即可得
,即可得![]() ,
,![]() ,
,![]() ,从而可求出平面
,从而可求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,进而可求二面角的余弦值.
,进而可求二面角的余弦值.
(1)证明:因为![]() 是等腰直角三角形,
是等腰直角三角形,![]() 为斜边,所以
为斜边,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解:由(1)知![]() ,
,![]() 平面
平面![]() ,则以
,则以![]() 为坐标原点,
为坐标原点,
![]() ,
,![]() 分别为
分别为![]() ,
,![]() 轴的正方向,过点
轴的正方向,过点![]() 平行于
平行于![]() 的直线为
的直线为![]() 轴,
轴,
建立如图所示的空间直角坐标系![]() .
.
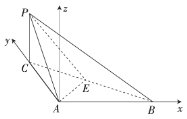
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则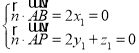 ,
,
令![]() ,得
,得![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则 ,
,
令![]() ,得
,得![]() ,则
,则![]() .
.
由图可知二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.