题目内容
向量
=(
,tanα),
=(cosα,1),且
∥
,则cos(
+α)=( )
| a |
| 1 |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
考点:三角函数的化简求值,平面向量共线(平行)的坐标表示
专题:三角函数的求值
分析:利用向量的平行列出方程,求出正弦函数值,利用诱导公式化简所求表达式求解即可.
解答:
解:由题意
∥
,
则tanα•cosα-
=0,化简得sinα=
,
而cos(
+α)=-sinα=-
,
故选B.
| a |
| b |
则tanα•cosα-
| 1 |
| 3 |
| 1 |
| 3 |
而cos(
| π |
| 2 |
| 1 |
| 3 |
故选B.
点评:本题考查向量的平行,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
设函数f(x)是定义在R上的奇函数,且满足f(3+x)=f(3-x),当x∈(0,3)时,f(x)=2x,则f(-5)=( )
| A、2 | ||
B、-
| ||
| C、-2 | ||
D、
|
在等比数列{an}中,a1+a2=20,a3+a4=80,则a7+a8=( )
| A、320 | B、640 |
| C、960 | D、1280 |
某校在暑假组织社会实践活动,将8名高一年级学生,平均分配甲、乙两家公司,其中两名英语成绩优秀学生不能分给同一个公司;另三名电脑特长学生也不能分给同一个公司,则不同的分配方案有( )
| A、36种 | B、38种 |
| C、108种 | D、114种 |
质检部门对某超市56种食用油(分别编号为1~56)进行抽样检查,用系统抽样的方法抽取了4种食用油,已知7号,35号被抽取到,那么另两种被抽取到的食用油编号是( )
| A、22号与49号 |
| B、21号与49号 |
| C、28号与42号 |
| D、21号与50号 |
已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=logax有三个不同的根,则a的范围为( )
| A、(2,4) | ||||
B、(2,2
| ||||
C、(
| ||||
D、(
|
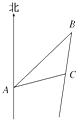 某海域内一观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东50°且与A相距80海里的位置B,经过1小时又测得该船已行驶到点A北偏东50°+θ其中sin θ=
某海域内一观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东50°且与A相距80海里的位置B,经过1小时又测得该船已行驶到点A北偏东50°+θ其中sin θ=