题目内容
 已知四棱锥
已知四棱锥![]() 中
中![]() 平面
平面![]() ,且
,且![]() ,底面为直角
,底面为直角![]()
![]()
![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:![]() // 平面
// 平面![]() ;
;
(2)求截面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
解法1:
以![]() 为原点,以
为原点,以![]() 分别为
分别为![]() 建立空间直角坐标系
建立空间直角坐标系![]() ,
,
由![]()
![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,
可得:

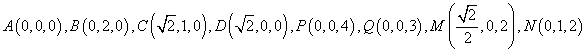 ,∴
,∴![]() ,
,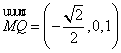 ………2分
………2分
设平面的![]() 的法向量为
的法向量为![]() ,
,
则有: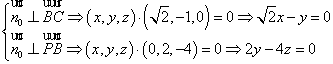
令![]() ,则
,则![]() , ……………3分
, ……………3分
∴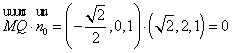 ,又
,又![]() 平面
平面![]()
∴![]() //平面
//平面![]() ……………4分
……………4分
(2)设平面的![]() 的法向量为
的法向量为![]() ,
,
又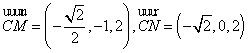
则有: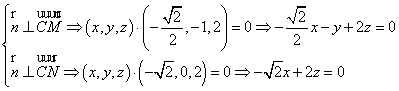
令![]() ,则
,则![]() , …………6分
, …………6分
又![]() 为平面
为平面![]() 的法向量,
的法向量,
∴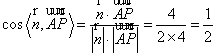 ,
,
又截面![]() 与底面
与底面![]() 所成二面角为锐二面角,
所成二面角为锐二面角,
∴截面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]() …………8分
…………8分
(3)∵![]() ,∴所求的距离
,∴所求的距离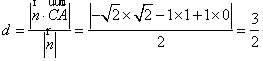 ………12分
………12分
解法2:(1)![]() //
//![]() ………………1分
………………1分
![]() ………………2分
………………2分
又![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() , ∴
, ∴![]() //平面
//平面![]() …………4分
…………4分
(2)易证:![]()
![]()
![]() ,
,
![]() ,
,
由(1)可知![]() 四点共面
四点共面
![]() ,………………6分
,………………6分
![]()
所以:![]() , 所以:
, 所以:![]()
故截面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]() …………8分
…………8分
(3)![]()
![]()
![]()
![]() …10分
…10分
![]() …12分
…12分

练习册系列答案
相关题目

 (本小题满分12分)已知四棱锥
(本小题满分12分)已知四棱锥 (必做题,每题10分)已知四棱锥
(必做题,每题10分)已知四棱锥 (1)求证:
(1)求证: (本小题满分12分)已知四棱锥
(本小题满分12分)已知四棱锥