题目内容
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列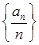 是递增数列;
是递增数列;
p4:数列{an+3nd}是递增数列.其中的真命题为( ).
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列
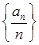 是递增数列;
是递增数列;p4:数列{an+3nd}是递增数列.其中的真命题为( ).
| A.p1,p2 | B.p3,p4 | C.p2,p3 | D.p1,p4 |
D
设an=a1+(n-1)d=dn+(a1-d).递增,p1真.
an+3nd=4dn+(a1-d)递增,p4为真命题.
若{an}的首项a1=-3,d=1,则an=n-4,
此时nan=n2-4n不单调,则p2为假命题.
若等差数列{an}满足an=n,则 =1为常数,p3错.因此p1,p4正确;p2,p3错误.
=1为常数,p3错.因此p1,p4正确;p2,p3错误.
an+3nd=4dn+(a1-d)递增,p4为真命题.
若{an}的首项a1=-3,d=1,则an=n-4,
此时nan=n2-4n不单调,则p2为假命题.
若等差数列{an}满足an=n,则
 =1为常数,p3错.因此p1,p4正确;p2,p3错误.
=1为常数,p3错.因此p1,p4正确;p2,p3错误.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
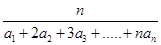 为{an}的“光阴”值,现知某数列的“光阴”值为Hn=
为{an}的“光阴”值,现知某数列的“光阴”值为Hn=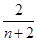 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________.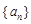 中,当
中,当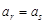
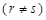 时,
时, ,则tan (a4+a6)=( ).
,则tan (a4+a6)=( ).

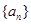 满足:
满足: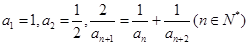 ,则
,则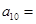 __________.
__________.