题目内容
已知函数 ,且
,且 .
.
(1)若 在
在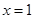 处取得极小值
处取得极小值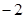 ,求函数
,求函数 的单调区间;
的单调区间;
(2)令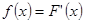 ,若
,若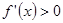 的解集为
的解集为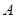 ,且满足
,且满足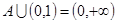 ,
,
求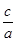 的取值范围。
的取值范围。
 ,且
,且 .
.(1)若
 在
在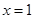 处取得极小值
处取得极小值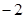 ,求函数
,求函数 的单调区间;
的单调区间;(2)令
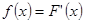 ,若
,若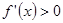 的解集为
的解集为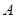 ,且满足
,且满足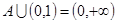 ,
,求
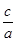 的取值范围。
的取值范围。: ,F'(-1)=0 则a-2b+c=0;
,F'(-1)=0 则a-2b+c=0;
(1)若F(x)在x=1处取得最小值-2,则F'(1)=0,a+2b+c=0,则b=0,c=-a。
F(1)=-2, ,则 a=3,c=-3。
,则 a=3,c=-3。
 ,x∈(-∞,-1)时,F'(x)>0,函数F(x)单调递增;
,x∈(-∞,-1)时,F'(x)>0,函数F(x)单调递增;
x∈(-1,1)时,F'(x)<0,函数F(x)单调递减;
x∈(1,∞)时,F'(x)>0,函数F(x)单调递增。
(2)令 ,
, ,
,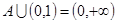 ,则
,则 ,即
,即 ,得
,得 即
即
 ,F'(-1)=0 则a-2b+c=0;
,F'(-1)=0 则a-2b+c=0;(1)若F(x)在x=1处取得最小值-2,则F'(1)=0,a+2b+c=0,则b=0,c=-a。
F(1)=-2,
 ,则 a=3,c=-3。
,则 a=3,c=-3。 ,x∈(-∞,-1)时,F'(x)>0,函数F(x)单调递增;
,x∈(-∞,-1)时,F'(x)>0,函数F(x)单调递增;x∈(-1,1)时,F'(x)<0,函数F(x)单调递减;
x∈(1,∞)时,F'(x)>0,函数F(x)单调递增。
(2)令
 ,
, ,
,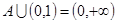 ,则
,则 ,即
,即 ,得
,得 即
即
略

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
 在点
在点 的切线方程为
的切线方程为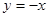
 的值;
的值;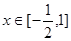 时,
时, 的图像与直线
的图像与直线 有两个不同的交点,求实数
有两个不同的交点,求实数 的取值范围;
的取值范围; ,不等式
,不等式 都成立.
都成立.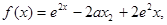 其中e为自然对数的底数。
其中e为自然对数的底数。 的导函数为
的导函数为 ,若函数
,若函数 的图象关于直线
的图象关于直线 对称,且
对称,且 .
. ,
, 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数 的极值。
的极值。 的导函数是
的导函数是 ,记
,记 ,
, ,
, ,则 ( )
,则 ( )



 的图象如右图所示,则下列说法正确的是 ( )
的图象如右图所示,则下列说法正确的是 ( )
 在
在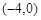 内单调递减
内单调递减 内单调递增
内单调递增 处取极大值
处取极大值 处取极小值
处取极小值 的导数为
的导数为 ,则
,则 的值为
的值为



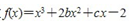 的图像在与x轴交点处的切线方程是y=5x-10
的图像在与x轴交点处的切线方程是y=5x-10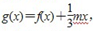 若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值。
若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值。