题目内容
17.设f(x)是一次函数,f(1)=1,且f(2),f(3)+1,f(5)成等差数列,若an=f(n),n∈N*.(1)求证:{an}是等差数列;
(2)在{an}每相邻的两项之间插入2个数,构成一个新的等差数列{bn},求数列{bn}的前n项和Bn.
分析 (1)设f(x)=ax+b,由于f(2),f(3)+1,f(5)成等差数列,可得2[f(3)+1]=f(2)+f(5),又f(1)=1,联立解得a,b,再利用等差数列的定义即可证明.
(2)在{an}每相邻的两项之间插入2个数,构成一个新的等差数列{bn},设公差为d.则在a1,a2,即1,3之间插入数2个数,构成一个新的等差数列{bn}的前4项,求出公差d即可得出.
解答 (1)证明:设f(x)=ax+b,
∵f(2),f(3)+1,f(5)成等差数列,∴2[f(3)+1]=f(2)+f(5),∴2(3a+b+1)=2a+b+5a+b,化为:a=2.
又f(1)=1,∴a+b=1,∴b=-1.
∴f(x)=2x-1.
∴an=f(n)=2n-1,
∴an+1-an=2(n+1)-1-(2n-1)=2,a1=1.
∴{an}是等差数列,首项为1,公差为2.
(2)在{an}每相邻的两项之间插入2个数,构成一个新的等差数列{bn},设公差为d.
则在a1,a2,即1,3之间插入数2个数,构成一个新的等差数列{bn}的前4项,
则b1=1,b4=3,∴3=1+3d,解得d=$\frac{2}{3}$,
∴bn=1+$\frac{2}{3}$(n-1)=$\frac{2}{3}$n+$\frac{1}{3}$.
∴数列{bn}的前n项和Bn=$\frac{n(1+\frac{2}{3}n+\frac{1}{3})}{2}$=$\frac{1}{3}{n}^{2}$+$\frac{2}{3}$n.
点评 本题考查了等差数列的定义及其通项公式前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知函数f(x)=sin(2x+φ)(|φ|<π)的图象过点P(0,$\frac{1}{2}$),如图,则φ的值为( )
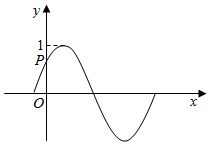

| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | -$\frac{π}{6}$或$\frac{5π}{6}$ |

 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.