题目内容

17．两个等差数列{an}：1，5，9，…和{bn}：3，10，17，…各取前200项，求公共项的总和．

分析 由已知得公共项构成的新数列{cn}是以c1=17为首项，d=28为公差的等差数列，从而cn=28n-11，求出a200=797，b200=1396，由cn=28n-11≤797，得到公共项28项，由此能求出公共项的总和．

解答 解：等差数列{an}：1，5，9，13，17，21，25，29，33，37，41，45，…
等差数列{bn}：3，10，17，24，31，38，45，…
∴公共项构成的新数列{cn}是以c1=17为首项，d=45-17=28为公差的等差数列，
∴cn=17+（n-1）×28=28n-11．
an=1+（n-1）（5-1）=4n-3，bn=3+（n-1）（10-3）=7n-4，
∴a200=4×200-3=797，b200=7×200-4=1396，
∴cn=28n-11≤797，解得n≤28$\frac{6}{7}$，
c28=773，c29=801，
∴公共项28项，
∴公共项的总和：${S}_{28}=28×17+\frac{28×27}{2}×28$=11060．

点评 本题考查等差数列的前n项和的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
7．三角形ABC的内角A，B的对边分别为a，b，若$acos（{π-A}）+bsin（{\frac{π}{2}+B}）=0$，则三角形ABC的形状为等腰三角形或直角三角形．
8．抛物线y2=2px（p＞0）的焦点为F，P为抛物线上一点，则以线段|PF|为直径的圆与y轴位置关系为（　　）
A．相交B．相离C．相切D．不确定
5．数列{an}中，a1=t，a2=t2，t∈（1，2），且an+1+tan-1=（t+1）an（n∈N，n≥2）．
（I）求证：数列{an+1-an}是等比数列，并求其通项公式；
（Ⅱ）若bn=$\frac{{{a}_{n}}^{2}+1}{2{a}_{n}}$（n∈N*），Sn为数列{bn}的前n项和，求证：Sn＜2n-${2}^{-\frac{n}{2}}$．
12．已知a=2-sin1，b=-$\frac{π}{6}$+sin$\frac{π}{12}$，c=-$\frac{π}{4}$+sin$\frac{π}{8}$，则（　　）
A．b＞c＞aB．a＞b＞cC．a＞c＞bD．b＞a＞c
2．等差数列{an}的各项均为正数，a1=3，前n项和为Sn，数列{bn}为等比数列，b1=1，且b2S2=4，b3S3=$\frac{15}{4}$．
（1）求数列{an}、{bn}的通项公式；
（2）数列{cn}满足：cn=（-1）n（an-2）bn+1，求数列{cn}的前n项和Tn．
9．已知tan（$\frac{π}{4}$+α）=-$\frac{1}{2}$．
（1）求tanα的值；
（2）求sin2α-cos2α的值．
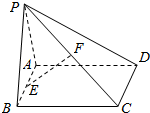6．如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，AB=1，BC=2，PA=2，E，F分别是AB，PC的中点．
（1）用向量法证明：AB⊥PD
（2）求丨EF丨
（3）求EF与PA所成的角的余弦值．
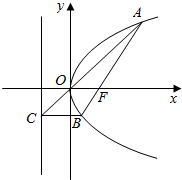7．过抛物线y2=2px的焦点F的直线和抛物线相交于A，B两点，如图所示．
（1）若A，B的纵坐标分别为y1，y2，求：y1y2=-p2；
（2）若直线AO与抛物线的准线相交于点C，求证：BC∥x轴．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网