题目内容

6．已知函数f（x）=axlnx+b（a，b∈R），若f（x）的图象在x=1处的切线方程为2x-y=0，则a+b=4．

分析 求出函数的导数，由题意可得f（1）=2，f′（1）=2，计算即可得到所求．

解答 解：f（x）=axlnx+b的导数为f′（x）=a（1+lnx），
由f（x）的图象在x=1处的切线方程为2x-y=0，
易知f（1）=2，即b=2，
f′（1）=2，即a=2，
则a+b=4．
故答案为：4．

点评 本题考查导数的运用：求切线的斜率，考查运算能力，正确求导和运用直线方程是解题的关键．

练习册系列答案
相关题目
16．已知函数f（x）=（2x2-x-1）ex，则方程${[{ef（x）}]^2}+tf（x）-9\sqrt{e}=0$（t∈R）的根的个数为（　　）
A．3B．2C．5D．4
17．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
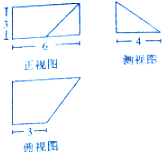
A．36B．30C．24D．20
14．已知数列{an}的前n项和${S_n}={n^2}+2n$，数列{bn}满足3n-1bn=a2n-1
（I）求an，bn；
（Ⅱ）设Tn为数列{bn}的前n项和，求Tn．
1．函数f（x）=sin（ωx+φ），（|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递增区间为（　　）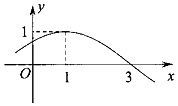
A．（-1+4kπ，1+4kπ），k∈ZB．（-3+8kπ，1+8kπ），k∈Z
C．（-1+4k，1+4k），k∈ZD．（-3+8k，1+8k），k∈Z
11．已知两条直线m，n和两个不同平面α，β，满足α⊥β，α∩β=l，m∥α，n⊥β，则（　　）
A．m∥nB．m⊥nC．m∥lD．n⊥l
18．若x1、x2、x3、…、x10的平均数为3，则3（x1-2）、3（x2-2）、3（x3-2）、…、3（x10-2）的平均数为（　　）
A．3B．9C．18D．27
15．已知f（x）=$\left\{\begin{array}{l}{3{x}^{2}+ln（\sqrt{1+{x}^{2}}+x），x≥0}\\{3{x}^{2}+ln（\sqrt{1+{x}^{2}}-x），x＜0}\end{array}\right.$，若f（x-1）＜f（2x+1），则x的取值范围为{x|x＞0，或x＜-2 }．
16．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的焦点坐标为（-4，0），（4，0），离心率为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网