题目内容
8.设Sn是等差数列{an}的前n项和,已知S3=6,a4=4.(1)求数列{an}的通项公式;
(2)若bn=3${\;}^{{a}_{n+1}}$-3${\;}^{{a}_{n}}$,求证:$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$<$\frac{1}{4}$.
分析 (1)根据等差数列的性质和求和公式可得到关于首项和公差的方程组,解得即可,
(2)先判断出{$\frac{1}{{b}_{n}}$}是等比数列,再根据等比数列的求和公式和放缩法即可证明.
解答 解:(1)设公差为d,则$\left\{\begin{array}{l}{{S}_{3}=3{a}_{1}+3d=6}\\{{a}_{4}={a}_{1}+3d=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=1}\end{array}\right.$,
∴an=n.
(2)证明:∵bn=3${\;}^{{a}_{n+1}}$-3${\;}^{{a}_{n}}$=3n+1-3n=2•3n,
∴$\frac{{b}_{n}}{{b}_{n+1}}$=$\frac{1}{3}$,
∴{$\frac{1}{{b}_{n}}$}是等比数列.
∵$\frac{1}{{b}_{1}}$=$\frac{1}{6}$,q=$\frac{1}{3}$,
∴$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$=$\frac{\frac{1}{6}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=$\frac{1}{4}$(1-$\frac{1}{{3}^{n}}$)<$\frac{1}{4}$.
点评 本题考查等差数列等比数列的通项和求和公式的运用,考查数列的求和方法,和放缩法,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.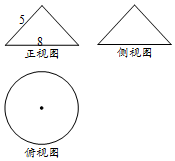 若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )
若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )
 若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )
若某几何体的三视图如图所示,其中正视图与侧视图是两个全等的等腰三角形,则此几何体的表面积是( )| A. | 36π | B. | 30π | C. | 24π | D. | 15π |
16.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(0)=2,则不等式f(x)-2ex<0的解集为( )
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
13.命题“?x∈R,使得x2<1”的否定是( )
| A. | ?x∈R,都有x2<1 | B. | ?x∈R,使得x2≥1 | ||
| C. | ?x∈R,都有x≤-1或x≥1 | D. | ?x∈R,使得x2>1 |
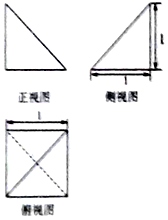
17.某棱锥的三视图如图所示,则该棱锥的外接球的表面积为( )

| A. | 3π | B. | 2π | C. | π | D. | 4π |