题目内容
(本小题满分12分)
已知抛物线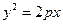 (
(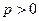 )的焦点为椭圆
)的焦点为椭圆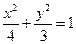 的右焦点,点
的右焦点,点 、
、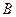 为抛物线上的两点,
为抛物线上的两点,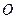 是抛物线的顶点,
是抛物线的顶点,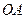 ⊥
⊥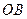 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线 过定点
过定点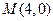 ;
;
(Ⅲ)设弦 的中点为
的中点为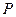 ,求点
,求点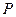 到直线
到直线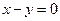 的距离的最小值.
的距离的最小值.
已知抛物线
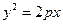 (
(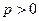 )的焦点为椭圆
)的焦点为椭圆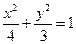 的右焦点,点
的右焦点,点 、
、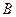 为抛物线上的两点,
为抛物线上的两点,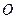 是抛物线的顶点,
是抛物线的顶点,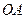 ⊥
⊥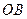 .
.(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证:直线
 过定点
过定点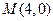 ;
;(Ⅲ)设弦
 的中点为
的中点为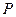 ,求点
,求点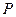 到直线
到直线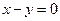 的距离的最小值.
的距离的最小值.解:(Ⅰ)椭圆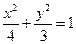 的右焦点
的右焦点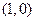 ,由题意知
,由题意知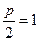 ∴
∴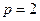 .……2分
.……2分
抛物线的标准方程为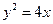 .……………………………………………………3分
.……………………………………………………3分
(Ⅱ)解法一:设直线 方程为
方程为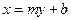 ,
,
 .
.
由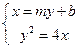 得
得 .…………………………………4分
.…………………………………4分
则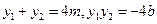 .…………………………………………………5分
.…………………………………………………5分
∵ ⊥
⊥ ,
,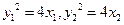 ,
,
∴ ,∴
,∴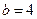 .……………………
.…………………… ……………7分
……………7分
∴直线 的方程为
的方程为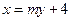 ,该直线恒过定点
,该直线恒过定点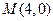 .……………………8分
.……………………8分
解法二:①当直线 的斜率不存在时,易求直线
的斜率不存在时,易求直线 的方程为
的方程为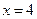 ,
,
直线 过定点
过定点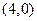 . ……………………………………………………………4分
. ……………………………………………………………4分
②当直线 的斜率存在时,设直线
的斜率存在时,设直线 的方程为:
的方程为: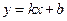
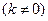 ,
,
由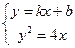 得
得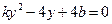 .
.
则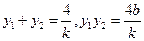 . ………………………………………………5分
. ………………………………………………5分
∵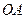 ⊥
⊥ ,
,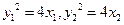 ,
,
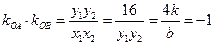 ,∴
,∴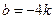 . ……………………………7分
. ……………………………7分
直线 的方程为
的方程为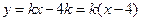 该直线恒过定点
该直线恒过定点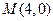 .……………8分
.……………8分
(Ⅲ)点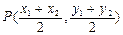 到直线
到直线
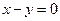 的距离:
的距离:
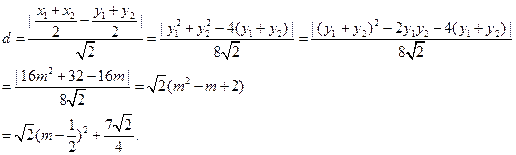 10分
10分
∴当
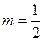 时,
时,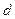 取最小值为
取最小值为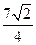 .……………………………………………12分
.……………………………………………12分
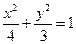 的右焦点
的右焦点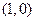 ,由题意知
,由题意知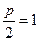 ∴
∴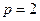 .……2分
.……2分抛物线的标准方程为
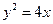 .……………………………………………………3分
.……………………………………………………3分
(Ⅱ)解法一:设直线
 方程为
方程为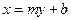 ,
,
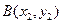 .
.由
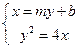 得
得 .…………………………………4分
.…………………………………4分则
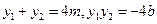 .…………………………………………………5分
.…………………………………………………5分∵
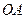 ⊥
⊥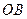 ,
,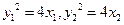 ,
,∴
 ,∴
,∴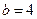 .……………………
.…………………… ……………7分
……………7分∴直线
 的方程为
的方程为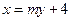 ,该直线恒过定点
,该直线恒过定点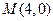 .……………………8分
.……………………8分解法二:①当直线
 的斜率不存在时,易求直线
的斜率不存在时,易求直线 的方程为
的方程为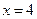 ,
,直线
 过定点
过定点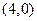 . ……………………………………………………………4分
. ……………………………………………………………4分②当直线
 的斜率存在时,设直线
的斜率存在时,设直线 的方程为:
的方程为: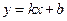
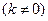 ,
,由
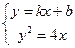 得
得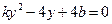 .
.则
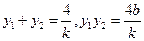 . ………………………………………………5分
. ………………………………………………5分∵
 ⊥
⊥ ,
,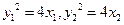 ,
,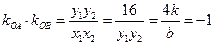 ,∴
,∴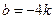 . ……………………………7分
. ……………………………7分直线
 的方程为
的方程为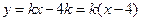 该直线恒过定点
该直线恒过定点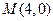 .……………8分
.……………8分(Ⅲ)点
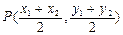 到直线
到直线
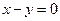 的距离:
的距离: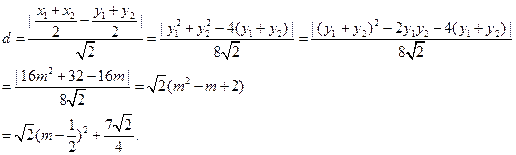 10分
10分∴当

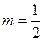 时,
时,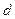 取最小值为
取最小值为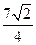 .……………………………………………12分
.……………………………………………12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
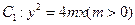 的准线与
的准线与 轴交于
轴交于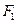 ,焦点为
,焦点为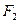 ;以
;以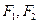 为焦点,离心率
为焦点,离心率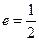 的椭圆
的椭圆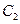 与抛物线
与抛物线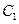 在
在 ,延长
,延长 交抛物线于点
交抛物线于点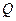 ,
,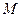 是抛物线
是抛物线 时,求椭圆
时,求椭圆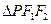 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求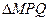 面积的最大值.
面积的最大值.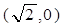 且与双曲线
且与双曲线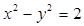 有且仅有一个公共点,则这样的直
有且仅有一个公共点,则这样的直 中,点P到两
中,点P到两 点
点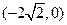 、
、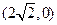 的距离之和等于6,设点P的轨迹为曲线
的距离之和等于6,设点P的轨迹为曲线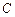 ,直线
,直线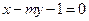 与曲线
与曲线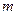 的值;
的值;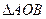 的面积最大,并求出面积的最大值.
的面积最大,并求出面积的最大值.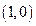 的距离比到直线
的距离比到直线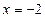 的距离少1,
的距离少1,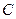 的轨迹的方程;
的轨迹的方程;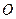 的两个不同点,直线
的两个不同点,直线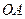 和
和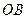 的倾
的倾 斜角分别为
斜角分别为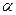 和
和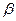 ,
, 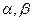 变化且
变化且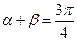 时,证明直线
时,证明直线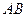 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.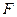 为抛物线
为抛物线 的焦点,与抛物线相切于点
的焦点,与抛物线相切于点 的直线
的直线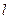 与
与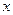 轴的交点为
轴的交点为 ,则
,则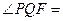 _________.
_________.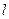 与抛物线
与抛物线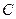 ,当直线
,当直线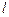 从
从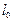 开始在平面上绕
开始在平面上绕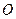 点按逆时针方向匀速旋转(旋转的角度不超过
点按逆时针方向匀速旋转(旋转的角度不超过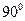 )时,它扫过的面积
)时,它扫过的面积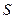 是时间
是时间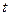 的函数,则函数图象大致是
的函数,则函数图象大致是
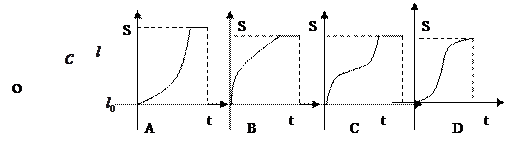
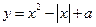 有两个交点,则
有两个交点,则 的取值范围是
的取值范围是  ,焦距为
,焦距为 ,则椭圆的标准方程为
,则椭圆的标准方程为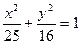 ;
;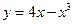 在点
在点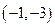 处的切线方程是
处的切线方程是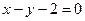 ;
;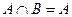 ,则
,则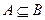 ”的逆否命题是:“若
”的逆否命题是:“若 ,则
,则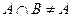 ”;
”;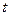 秒时距水面高度
秒时距水面高度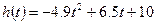 (单位:米),则该运动员的初速度为
(单位:米),则该运动员的初速度为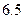 (米/秒);
(米/秒);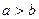 ”是“
”是“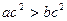 ”的充分条件。
”的充分条件。