题目内容
已知动点C到定点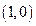 的距离比到直线
的距离比到直线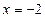 的距离少1,
的距离少1,
(1)求动点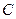 的轨迹的方程;
的轨迹的方程;
(2)设A、B是轨迹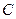 上异于原点
上异于原点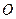 的两个不同点,直线
的两个不同点,直线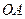 和
和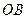 的倾
的倾 斜角分别为
斜角分别为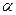 和
和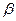 ,
,
当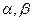 变化且
变化且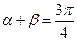 时,证明直线
时,证明直线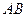 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
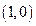 的距离比到直线
的距离比到直线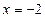 的距离少1,
的距离少1,(1)求动点
 的轨迹的方程;
的轨迹的方程;(2)设A、B是轨迹
 上异于原点
上异于原点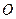 的两个不同点,直线
的两个不同点,直线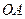 和
和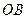 的倾
的倾 斜角分别为
斜角分别为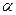 和
和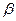 ,
, 当
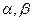 变化且
变化且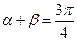 时,证明直线
时,证明直线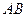 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.(1)
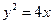
(2)
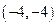
解:(1)如图,设 为动圆圆心,由抛物线的定义知,点
为动圆圆心,由抛物线的定义知,点 的轨迹为抛物线,
的轨迹为抛物线,

其中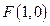 为焦点,
为焦点,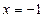 为准线,
为准线,
所以轨迹方程为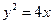 ; ┅┅┅┅3分
; ┅┅┅┅3分
(2)如图,设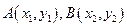 ,由题意得
,由题意得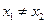
(否则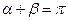 )且
)且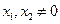 所以直线
所以直线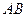 的斜率存在,┅┅┅┅4分
的斜率存在,┅┅┅┅4分
设其方程为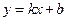 ,显然
,显然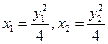 ,将
,将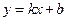 与
与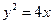 联立消去
联立消去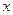 ,
,
得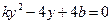 由韦达定理知
由韦达定理知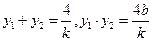 ①┅┅┅┅6分
①┅┅┅┅6分
由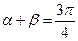 ,得
,得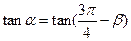 =
=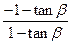 ,得
,得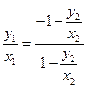 ┅┅┅┅9分
┅┅┅┅9分
 整理化简可得:
整理化简可得: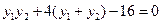 ,
,
将①式代入上式所以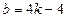 ┅11分
┅11分
此时,直线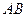 的方程可表示为
的方程可表示为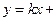
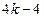 即
即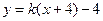
所以直线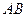 恒过定点
恒过定点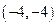 ┅┅┅┅13分
┅┅┅┅13分
 为动圆圆心,由抛物线的定义知,点
为动圆圆心,由抛物线的定义知,点 的轨迹为抛物线,
的轨迹为抛物线,
其中
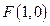 为焦点,
为焦点,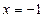 为准线,
为准线, 所以轨迹方程为
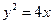 ; ┅┅┅┅3分
; ┅┅┅┅3分(2)如图,设
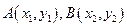 ,由题意得
,由题意得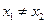
(否则
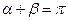 )且
)且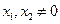 所以直线
所以直线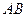 的斜率存在,┅┅┅┅4分
的斜率存在,┅┅┅┅4分设其方程为
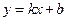 ,显然
,显然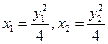 ,将
,将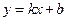 与
与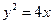 联立消去
联立消去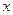 ,
,得
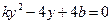 由韦达定理知
由韦达定理知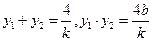 ①┅┅┅┅6分
①┅┅┅┅6分由
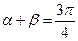 ,得
,得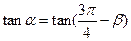 =
=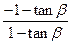 ,得
,得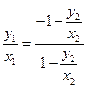 ┅┅┅┅9分
┅┅┅┅9分 整理化简可得:
整理化简可得: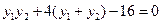 ,
,将①式代入上式所以
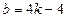 ┅11分
┅11分此时,直线
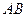 的方程可表示为
的方程可表示为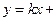
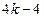 即
即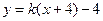
所以直线
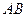 恒过定点
恒过定点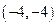 ┅┅┅┅13分
┅┅┅┅13分
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
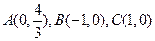 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。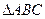 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。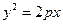 (
(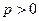 )的焦点为椭圆
)的焦点为椭圆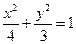 的右焦点,点
的右焦点,点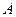 、
、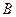 为抛物线上的两点,
为抛物线上的两点,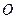 是抛物线的顶点,
是抛物线的顶点,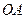 ⊥
⊥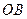 .
. 过定点
过定点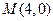 ;
;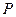 ,求点
,求点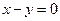 的距离的最小值.
的距离的最小值. -1,m
-1,m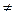 0).
0).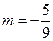 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线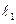 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为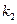 ,求证
,求证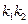 为定值;
为定值; ,且
,且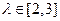 ,求
,求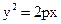 (p>0)过点C,求焦点F到直线AB的距离.
(p>0)过点C,求焦点F到直线AB的距离. 的一条准线与抛物线
的一条准线与抛物线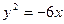 的准线重合,则该双曲线的离心率为 ( )
的准线重合,则该双曲线的离心率为 ( )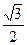 B
B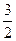 C
C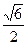 D
D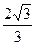
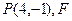 为抛物线
为抛物线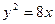 的焦点,
的焦点,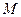 为此抛物线上的点,且使
为此抛物线上的点,且使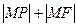 的值最小,则
的值最小,则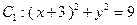 外切且与圆
外切且与圆 内切的动圆圆心轨迹
内切的动圆圆心轨迹