题目内容
经过椭圆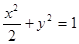 的右焦点作倾斜角为
的右焦点作倾斜角为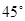 的直线
的直线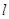 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则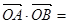 ( )
( )
A. -3
B.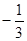
C. -3或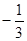
D.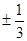
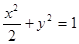 的右焦点作倾斜角为
的右焦点作倾斜角为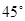 的直线
的直线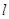 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则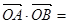 ( )
( )A. -3
B.
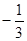
C. -3或
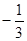
D.
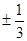
B
试题分析:由椭圆方程为
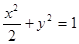 得a2=2,b2=1,c2=a2-b2=1,焦点为(±1,0).
得a2=2,b2=1,c2=a2-b2=1,焦点为(±1,0).设直线
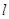 的方程为y=x-1.与椭圆方程联立
的方程为y=x-1.与椭圆方程联立 得:
得: ,设A(x1,y1),B(x2,y2),则x1•x2=0,x1+x2=
,设A(x1,y1),B(x2,y2),则x1•x2=0,x1+x2= ,y1y2=(x1-1)(x2-1)=x1x2-(x1+x2)+1=1-
,y1y2=(x1-1)(x2-1)=x1x2-(x1+x2)+1=1- =
= ,
,所以
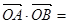 =x1x2+y1y2=
=x1x2+y1y2= 。故选B
。故选B点评:本题主要考查了椭圆的应用.当涉及过焦点的直线时,常需设出直线方程与椭圆方程联立利用韦达定理来解决.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
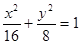 两焦点为
两焦点为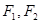 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点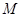 ,使得
,使得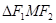 为直角三角形;
为直角三角形;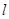 过抛物线
过抛物线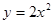 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于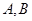 两点,则
两点,则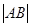 的最小值为2;
的最小值为2;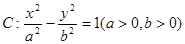 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为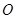 为坐标原点,则
为坐标原点,则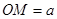 ;
;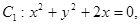 ⊙
⊙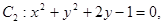 则这两圆恰有2条公切线。
则这两圆恰有2条公切线。 的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
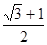



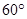 ,则双曲线C的离心率为 .
,则双曲线C的离心率为 .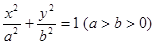 的右焦点F为
的右焦点F为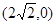 ,G上的点到点F的最大距离为
,G上的点到点F的最大距离为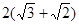 ,斜率为1的直线
,斜率为1的直线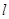 与椭圆G交与
与椭圆G交与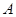 、
、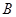 两点,以AB为底边作等腰三角形,顶点为P(-3,2)
两点,以AB为底边作等腰三角形,顶点为P(-3,2)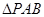 的面积。
的面积。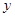 轴的负半轴上,过点
轴的负半轴上,过点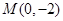 作直线
作直线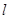 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足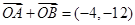 ,
,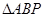 面积的的最大值.
面积的的最大值.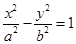 的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是
的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是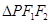 的重心,若
的重心,若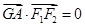 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
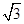
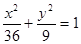 的一条弦被
的一条弦被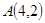 平分,那么这条弦所在的直线方程是 ( )
平分,那么这条弦所在的直线方程是 ( )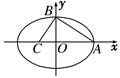
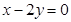
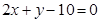
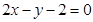
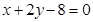
 的准线与双曲线
的准线与双曲线 的右准线重合,则
的右准线重合,则 的值是 ( )
的值是 ( ) 


