题目内容
F1、F2分别是双曲线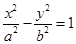 的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是
的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是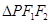 的重心,若
的重心,若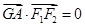 ,则双曲线的离心率是( )
,则双曲线的离心率是( )
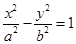 的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是
的左、右焦点,A是其右顶点,过F2作x轴的垂线与双曲线的一个交点为P,G是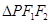 的重心,若
的重心,若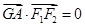 ,则双曲线的离心率是( )
,则双曲线的离心率是( )| A.2 | B. | C.3 | D.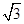 |
C
试题分析:求出F1,F2、A、G、P的坐标,由
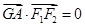 ,得GA⊥F1F2,故G、A 的横坐标相同,可得
,得GA⊥F1F2,故G、A 的横坐标相同,可得 =a,从而求出双曲线的离心率. 由题意可得 F1(-c,0),F2 (c,0),A(a,0).把x=c代入双曲线方程可得y=±
=a,从而求出双曲线的离心率. 由题意可得 F1(-c,0),F2 (c,0),A(a,0).把x=c代入双曲线方程可得y=± ,故一个交点为P(c,
,故一个交点为P(c, ),由三角形的重心坐标公式可得G(
),由三角形的重心坐标公式可得G( ,
, ).若
).若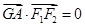 ,则 GA⊥F1F2,∴G、A 的横坐标相同,∴
,则 GA⊥F1F2,∴G、A 的横坐标相同,∴ ="a,"
="a,"  =3,c=9,故选 C.
=3,c=9,故选 C.点评:解决该试题的关键是求出重心G的坐标,同时能利用向量的数量积为零,来表示向量的垂直关系,进而求解得到。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
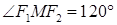 ,则双曲线离心率为
,则双曲线离心率为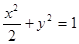 的右焦点作倾斜角为
的右焦点作倾斜角为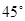 的直线
的直线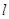 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则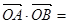 ( )
( )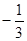
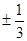
 和双曲线
和双曲线 ,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )
,有相同的焦点,则椭圆与双曲线的离心率的平方和为( )

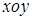 中,
中,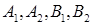 为椭圆
为椭圆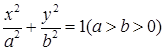 的
的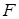 为其右焦点,直线
为其右焦点,直线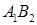 与直线
与直线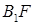 相交于点T,线段
相交于点T,线段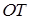 与椭圆的交点
与椭圆的交点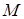 恰为线段
恰为线段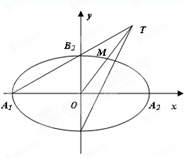
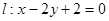 关于原点对称的直线为
关于原点对称的直线为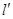 ,若
,若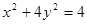 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为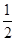 的点M的个数为
的点M的个数为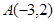 的抛物线的标准方程是
的抛物线的标准方程是  ,则它的一个焦点到一条渐进线的距离是( )
,则它的一个焦点到一条渐进线的距离是( ) D. 12
D. 12