题目内容
(12分)抛物线的顶点在坐标原点,焦点在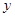 轴的负半轴上,过点
轴的负半轴上,过点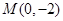 作直线
作直线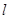 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足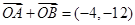 ,
,
(1)求抛物线的方程
(2)当抛物线上的一动点P从A运动到B时,求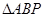 面积的的最大值.
面积的的最大值.
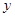 轴的负半轴上,过点
轴的负半轴上,过点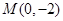 作直线
作直线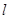 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足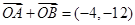 ,
,(1)求抛物线的方程
(2)当抛物线上的一动点P从A运动到B时,求
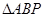 面积的的最大值.
面积的的最大值.(1)  (2)
(2) 
 (2)
(2) 
试题分析:(1)设直线的方程为
 与抛物线
与抛物线 联立消去
联立消去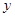 得
得
 又
又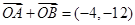

 ,
, 得
得 解得
解得
(2)底确定当高最大时面积最大,此时的高就是平行于AB且与抛物线相切的直线和直线AB间的距离设直线方程为
 利用相切条件即
利用相切条件即 得
得
于是

点评:直线和圆锥曲线的位置关系通常联立方程利用韦达定理

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
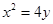 的准线方程为 .
的准线方程为 .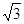 ) ,渐近线方程为
) ,渐近线方程为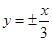 ,则此双曲线的方程为 _.
,则此双曲线的方程为 _.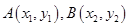 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: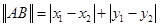 .给出下列三个命题:
.给出下列三个命题: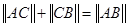 ;
;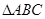 中,若∠C=90°,则
中,若∠C=90°,则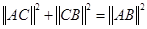 ;
;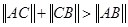 .
.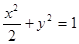 的右焦点作倾斜角为
的右焦点作倾斜角为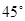 的直线
的直线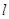 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则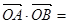 ( )
( )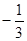
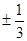
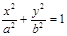 (
(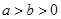 )
) ,M,N是椭圆上关于原点对称的两点,P是椭圆上任意一点,且直线PM,PN的斜率分别为
,M,N是椭圆上关于原点对称的两点,P是椭圆上任意一点,且直线PM,PN的斜率分别为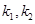 ,
, =
=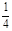 ,则椭圆的离心率为( )
,则椭圆的离心率为( )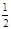
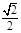
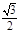
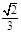
 中,
中,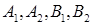 为椭圆
为椭圆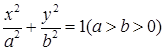 的
的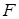 为其右焦点,直线
为其右焦点,直线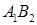 与直线
与直线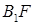 相交于点T,线段
相交于点T,线段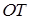 与椭圆的交点
与椭圆的交点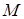 恰为线段
恰为线段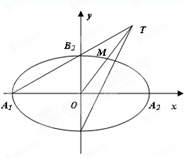
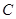 :
: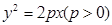 过点
过点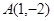 .(1)求抛物线
.(1)求抛物线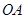 (
(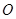 为坐标原点)的直线
为坐标原点)的直线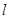 ,使得直线
,使得直线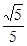 ?若存在,求出直线
?若存在,求出直线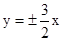 ,则其离心率是为 .
,则其离心率是为 .