题目内容
.（本题满分13分）已知椭圆C的中点在原点，焦点在x轴上，离心率等于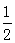
，它的一个顶点恰好是抛物线
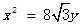的焦点．
(1)求椭圆C的方程;
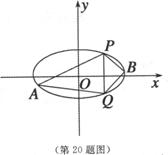
(2)P(2，3)，Q(2，-3)是椭圆上两点，A、B是椭圆上位于直线PQ两侧的两动点，若直线AB的斜率为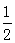，求四边形APBQ面积的最大值．
【答案】
解：(1）设
方程为
，则
.
由
，得
∴椭圆C的方程为
.
………………………………… 5分
(2)设
，直线
的方程为
，
代入，得
由
，解得
…………………………………9分
由韦达定理得
.
四边形
的面积
∴当
，
. ………………………………… 13分
【解析】略
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
，
，
. 
，
； (2) 若
，求
的取值范围.
的三个内角
依次成等差数列．
，试判断
，求
中，
，
，
分别为内角
，
，
所对的边，且满足
．
，且
，
，求
的值．
展开式中，求：
平面ABCD，AD//BC//FE，AB
AD.
？若存在，试确定点M的位置；若不存在，请说明理由.